题目内容
(12分)设直线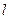 与圆
与圆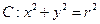 交于A、B两点,O为坐标原点,已知A点的坐标为
交于A、B两点,O为坐标原点,已知A点的坐标为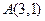 .(Ⅰ)当原点O到直线
.(Ⅰ)当原点O到直线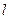 的距离为
的距离为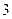 时,求直线
时,求直线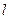 方程;(Ⅱ)当
方程;(Ⅱ)当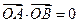 时,求直线
时,求直线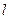 的方程。
的方程。
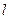 与圆
与圆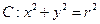 交于A、B两点,O为坐标原点,已知A点的坐标为
交于A、B两点,O为坐标原点,已知A点的坐标为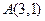 .(Ⅰ)当原点O到直线
.(Ⅰ)当原点O到直线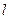 的距离为
的距离为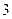 时,求直线
时,求直线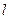 方程;(Ⅱ)当
方程;(Ⅱ)当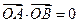 时,求直线
时,求直线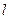 的方程。
的方程。

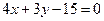
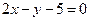 或
或 .
.(Ⅰ)∵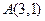 在圆C上,∴
在圆C上,∴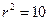 ,圆的方程为
,圆的方程为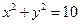
设直线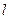 的方程为:
的方程为: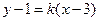 ,即
,即 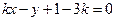
由条件得: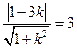
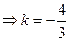 此时直线
此时直线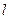 的方程为
的方程为 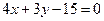
当直线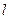 的斜率不存在时,直线
的斜率不存在时,直线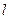 ;
;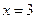 也符合要求
也符合要求
∴直线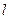 的方程为
的方程为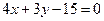 或
或 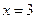 . -------------(6分)
. -------------(6分)
(Ⅱ)由条件得OA的斜率为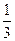 ∵
∵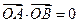 ∴OB的斜率为
∴OB的斜率为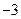 ,
,


OB所在直线的方程为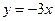
由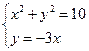 解得B点的坐标为
解得B点的坐标为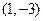 或
或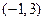
由两点式求得直线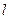 的方程为
的方程为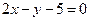 或
或 .----(12分)
.----(12分)
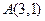 在圆C上,∴
在圆C上,∴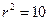 ,圆的方程为
,圆的方程为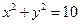
设直线
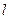 的方程为:
的方程为: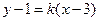 ,即
,即 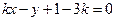
由条件得:
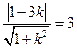
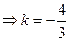 此时直线
此时直线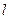 的方程为
的方程为 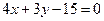
当直线
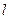 的斜率不存在时,直线
的斜率不存在时,直线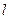 ;
;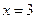 也符合要求
也符合要求∴直线
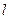 的方程为
的方程为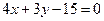 或
或 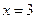 . -------------(6分)
. -------------(6分)(Ⅱ)由条件得OA的斜率为
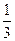 ∵
∵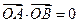 ∴OB的斜率为
∴OB的斜率为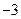 ,
,


OB所在直线的方程为
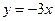
由
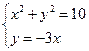 解得B点的坐标为
解得B点的坐标为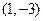 或
或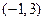
由两点式求得直线
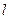 的方程为
的方程为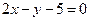 或
或 .----(12分)
.----(12分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
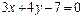 的倾斜角相等,并且与两坐标轴围成的三角形面积等于24,求直线l的方程.
的倾斜角相等,并且与两坐标轴围成的三角形面积等于24,求直线l的方程.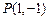 有一条直线l,它夹在两条直线
有一条直线l,它夹在两条直线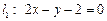 与
与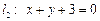 之间的线段恰被点P平分,求直线l的方程.
之间的线段恰被点P平分,求直线l的方程. 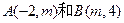 的直线与直线
的直线与直线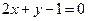 平行,则实数
平行,则实数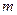 的值为
的值为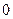
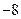
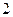
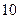
 经过第一、二、三象限,则( )
经过第一、二、三象限,则( ) 、
、 ,若
,若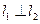 ,则直线
,则直线 的一个方向向量为
的一个方向向量为 .
.