题目内容
设函数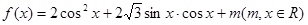 .
.
(1)求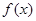 的最小正周期;
的最小正周期;
(2)当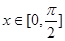 时,求实数
时,求实数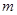 的值,使函数
的值,使函数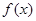 的值域恰为
的值域恰为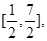 并求此时
并求此时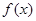 在
在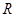 上的对称中心.
上的对称中心.
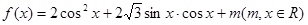 .
.(1)求
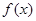 的最小正周期;
的最小正周期;(2)当
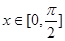 时,求实数
时,求实数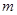 的值,使函数
的值,使函数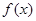 的值域恰为
的值域恰为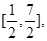 并求此时
并求此时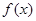 在
在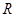 上的对称中心.
上的对称中心.(1) ;(2)
;(2)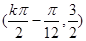 .
.
 ;(2)
;(2)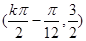 .
.试题分析:(1)将
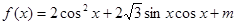 降次化一,可化为
降次化一,可化为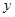
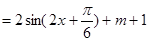 的形式,由此即可求得其周期.
的形式,由此即可求得其周期.(2)在(1)中得,
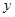
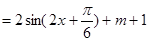
当
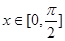 时,可以得到
时,可以得到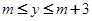 .又
.又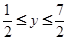 ,所以
,所以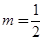 .这样
.这样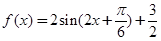 .
.令
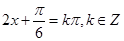 ,得
,得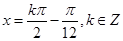 ,从而得对称中心为
,从而得对称中心为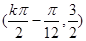 .
.试题解析:(1)
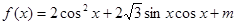
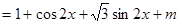
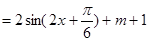 ∴函数
∴函数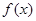 的最小正周期T=
的最小正周期T= 。
。(2)
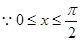
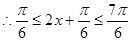
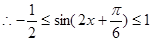
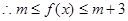 又
又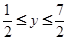 ,所以
,所以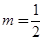 ,所以
,所以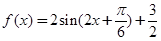 .
.令
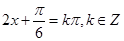 ,解得
,解得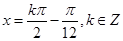 ,对称中心为
,对称中心为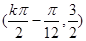 .
.
练习册系列答案
相关题目
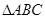 中,角
中,角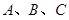 所对的边为
所对的边为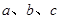 ,且满足
,且满足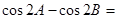
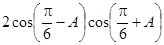
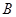 的值;
的值;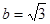 且
且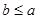 ,求
,求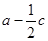 的取值范围.
的取值范围.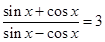 .
.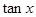 的值;
的值;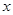 是第三象限的角,化简三角式
是第三象限的角,化简三角式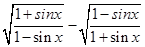 ,并求值.
,并求值. 的部分图象如图所示,若
的部分图象如图所示,若 ,则
,则 ( )
( )




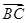 =λ
=λ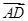 (λ∈R),|
(λ∈R),|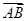 |=|
|=|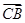 -
-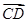 |=2
|=2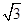 ,且△BCD是以BC为斜边的直角三角形,则
,且△BCD是以BC为斜边的直角三角形,则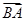 的值为__________.
的值为__________.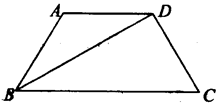
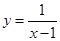 的图像与函数
的图像与函数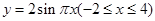 的图像所有交点的横坐标之和等于( )
的图像所有交点的横坐标之和等于( )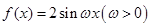 的图象在
的图象在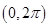 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则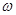 的取值范围是( )
的取值范围是( )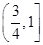
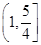
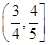
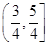
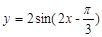 的图象关于点P
的图象关于点P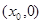 成中心对称,若
成中心对称,若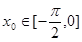 ,则
,则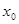 =________.
=________.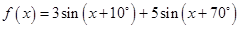 的最大值是( )
的最大值是( )