题目内容
函数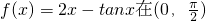 上的最大值为________.
上的最大值为________.
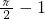
分析:求出函数的导数,令导数大于0,求出函数的单调区间,再由单调性判断出函数的最值并求出.
解答:∵f(x)=2x-tanx,
∴
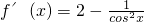 =2-
=2-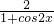
令f'(x)=0得1+cos2x=1
又x∈
 ,得x=
,得x= ,故当x∈
,故当x∈ 时导数为正,当x∈
时导数为正,当x∈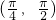 时,导数为负
时,导数为负故函数在
 上增,在
上增,在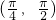 上减,所以当x=
上减,所以当x= 时函数值取到最大值,最大值为
时函数值取到最大值,最大值为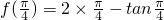 =
=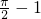 .
.故答案为
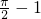
点评:本题考查利用导数求闭区间上函数的最值,求解本题的关键是正确求出函数的导数根据导数判断出最值在何处取到,本题中正切函数的导数求导方法是这样的,先切化弦再利用商的导数法则求导.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
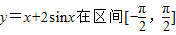 上的最大值为 .
上的最大值为 .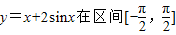 上的最大值为 .
上的最大值为 .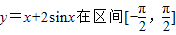 上的最大值为 .
上的最大值为 .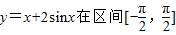 上的最大值为 .
上的最大值为 .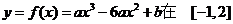 上的最大值为3,最小值为
上的最大值为3,最小值为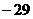 ,求
,求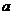 ,
,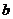 的值。
的值。