题目内容
函数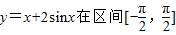
上的最大值为 ．
【答案】分析：用导数判断函数的单调性，由单调性可求最大值．
解答：解：y′=1+2cosx，当x∈[-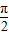
，
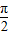]时，y′＞0，
所以y=x+2sinx在[-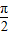
，
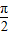]上单调递增，
所以当x=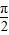
时，y=x+2sinx取得最大值为：
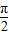+2sin
=
+2．
故答案为：
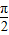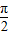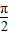+2．
点评：本题考查函数的单调性，对于由不同类型的函数构成的函数最值问题，常用函数的性质解决．
解答：解：y′=1+2cosx，当x∈[-
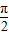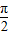，]时，y′＞0，所以y=x+2sinx在[-
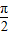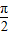，]上单调递增，所以当x=
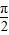时，y=x+2sinx取得最大值为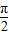：+2sin=+2．故答案为：
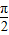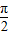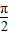+2．点评：本题考查函数的单调性，对于由不同类型的函数构成的函数最值问题，常用函数的性质解决．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
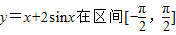上的最大值为 ．
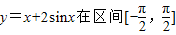上的最大值为 ．
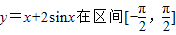上的最大值为 ．
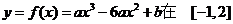上的最大值为3，最小值为
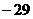，求
，
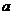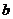的值。