题目内容
平面内给定两个向量
=(3,1),
=(-1,2)
(1)求|3
+2
|;
(2)若(
+k
)∥(2
-
),求实数k的值.
| a |
| b |
(1)求|3
| a |
| b |
(2)若(
| a |
| b |
| a |
| b |
分析:(1)利用向量的运算法则和模的计算公式即可得出.
(2)利用向量共线定理即可得出.
(2)利用向量共线定理即可得出.
解答:解:(1)由条件知:3
+2
=(7,7),
故|3
+2
|=
=7
.
(2)
+k
=(3,1)+k(-1,2)=(3-k,1+2k),2
-
=(7,0).
∵(
+k
)∥(2
-
),
∴(3-k)•0-7(1+2k)=0,
解得k=-
.
| a |
| b |
故|3
| a |
| b |
| 72+72 |
| 2 |
(2)
| a |
| b |
| a |
| b |
∵(
| a |
| b |
| a |
| b |
∴(3-k)•0-7(1+2k)=0,
解得k=-
| 1 |
| 2 |
点评:熟练掌握向量的运算法则和模的计算公式、向量共线定理是解题的关键.

练习册系列答案
相关题目
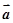 是已知的平面向量且
是已知的平面向量且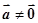 ,关于向量
,关于向量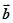 ,总存在向量
,总存在向量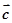 ,使
,使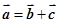 ;
;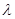 和
和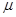 ,使
,使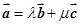 ;
;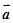 是已知的平面向量且
是已知的平面向量且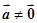 ,关于向量
,关于向量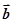 ,总存在向量
,总存在向量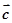 ,使
,使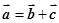 ;
;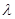 和
和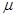 ,使
,使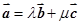 ;
;