题目内容
14.在递增的等比数列{an}中,已知a1+an=34,a3•an-2=64,且前n项和为Sn=42,则n=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由题意易得a1和an是方程x2-34x+64=0的两根,结合数列递增可解得a1=2,an=32,再由Sn=42的q,可得n值.
解答 解:由等比数列的性质可得a1an=a3•an-2=64,
又a1+an=34,
∴a1和an是方程x2-34x+64=0的两根,
解方程可得x=2或x=32,
∵等比数列{an}递增,∴a1=2,an=32,
∵Sn=42,∴$\frac{{a}_{1}-{a}_{n}q}{1-q}$=$\frac{2-32q}{1-q}$=42,
解得q=4,∴32=2×4n-1,解得n=3
故选:A
点评 本题考查等比数列的求和公式和通项公式,涉及等比数列的性质和韦达定理,属基础题.

练习册系列答案
相关题目
6.圆(x-a)2+y2=1与直线y=x相切于第三象限,则a=( )
| A. | -2 | B. | 2 | C. | $-\sqrt{2}$ | D. | $\sqrt{2}$ |
4.在区间[0,2]上随机取一个实数x,则事件“3x-1<0”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
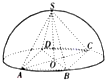 如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
如图,半球O内有一内接四棱锥S-ABCD,底面ABCD为正方形,SO⊥底面ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.