题目内容
给出下列命题:
①不等式
≥2的解集是{x|x≤
};
②若α,β是第一象限角,且α>β,则sinα>sinβ;
③tan20°+tan40°+
tan20°tan40°=
;
④f(x)=2sin(3x+1)的图象可由y=2sin3x的图象向左平移1个单位得到;
⑤函数f(x)=
的值域是(-
,
).
其中正确的命题的序号是
①不等式
| 1 |
| x |
| 1 |
| 2 |
②若α,β是第一象限角,且α>β,则sinα>sinβ;
③tan20°+tan40°+
| 3 |
| 3 |
④f(x)=2sin(3x+1)的图象可由y=2sin3x的图象向左平移1个单位得到;
⑤函数f(x)=
| cos2x |
| cosx-sinx |
| 2 |
| 2 |
其中正确的命题的序号是
③⑤
③⑤
(要求写出所有正确命题的序号).分析:根据分式不等式的解法,解出不等式可以判断①的真假;根据正弦函数的单调性是一个局部性质,在第一象限三角函数不具备单调性,可以判断②的真假;根据两角和的余切公式,变形后,可以判断③的真假;根据函数图象的平移变换法则,可以判断④的真假;根据正弦型函数的性质,求出函数的值域,可以判断⑤的真假,进而得到答案.
解答:解:不等式
≥2的解集是{x|0<x≤
},故①错误;
若α,β是第一象限角,且α>β,则与α,β终边相同的锐角大小不能确定,则sinα与sinβ无法比较大小,故②错误;
tan20°+tan40°+
tan20°tan40°=
成立,故③正确;
f(x)=2sin(3x+1)的图象可由y=2sin3x的图象向左平移
个单位得到,故④错误;
函数f(x)=
=cosx+sinx=
sin(x+
),其值域是(-
,
),故⑤正确;
故答案为:③⑤
| 1 |
| x |
| 1 |
| 2 |
若α,β是第一象限角,且α>β,则与α,β终边相同的锐角大小不能确定,则sinα与sinβ无法比较大小,故②错误;
tan20°+tan40°+
| 3 |
| 3 |
f(x)=2sin(3x+1)的图象可由y=2sin3x的图象向左平移
| 1 |
| 2 |
函数f(x)=
| cos2x |
| cosx-sinx |
| 2 |
| π |
| 4 |
| 2 |
| 2 |
故答案为:③⑤
点评:本题考查的知识点是命题的真假判断与应用,分式不等式的解法,三角函数的单调性,两角和的正切公式,函数图象的平移变换,三角函数的值域,其中根据上述基本知识点,分别判断出题目中各个命题的真假,是解答本题的关键.

练习册系列答案
相关题目
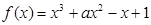 ,给出下列命题:
,给出下列命题: =0一定有三个不等的实数根.
=0一定有三个不等的实数根.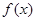 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题: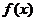 =x3+ax2-x+1,给出下列命题:
=x3+ax2-x+1,给出下列命题: