题目内容
已知点![]()
![]() )都在函数
)都在函数![]() 的图象上.
的图象上.
(1)若数列![]() 是等差数列,求证数列
是等差数列,求证数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 的前
的前![]() 项和为
项和为![]() =
=![]() ,过点
,过点![]() 的直线与两坐标轴所围成三角 形面积为
的直线与两坐标轴所围成三角 形面积为![]() ,求使
,求使![]() 对
对![]()
![]() 恒成立的实数
恒成立的实数![]() 的取值范围.
的取值范围.
(Ⅰ)见解析 (Ⅱ) ![]()
解析:
(Ⅰ)因为数列![]() 是等差数列,故设公差为
是等差数列,故设公差为![]() ,
,
则![]() 对
对![]() N
N![]() 恒成立.依题意
恒成立.依题意
![]() ,
,![]() .
.
由![]() ,所以
,所以 是定值,
是定值,
从而数列![]() 是等比数列. …………4分
是等比数列. …………4分
(Ⅱ)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时也适合此式,即数列
时也适合此式,即数列![]() 的通项公式是
的通项公式是![]() . ………………7分
. ………………7分
由![]() ,数列
,数列![]() 的通项公式是
的通项公式是![]() . ……………8分
. ……………8分
所以![]() ,过这两点的直线方程是
,过这两点的直线方程是![]() ,该直线与坐标轴的交点是
,该直线与坐标轴的交点是![]() 和
和![]() .
.
![]() . ……………10分
. ……………10分
因为![]() .
.
即数列![]() 的各项依次单调递减,所以要使
的各项依次单调递减,所以要使![]() 对
对![]() N
N![]() 恒成立,只要
恒成立,只要![]() ,又
,又![]() ,可得
,可得![]() 的取值范围是
的取值范围是![]() .
.
故实数![]() 的取值范围是
的取值范围是![]() . …………12分
. …………12分

练习册系列答案
相关题目
 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数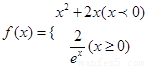 ,则
,则 的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数
的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数 的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数
的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数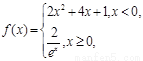 则
则 的“友好点对”、
的“友好点对”、
 的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数
的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数 的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数
的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数 则
则 的“友好点对”有
的“友好点对”有  满足条件:①
满足条件:① 的图象上;②
的图象上;②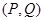 是函数
是函数 看作同一个“友好点对”).已知函数
看作同一个“友好点对”).已知函数 ,则
,则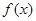 的“友好点对”有 个.
的“友好点对”有 个.