题目内容
已知点M为等边三角形ABC的中心,AB=2,直线l过点M交边AB于点P,交边AC于点Q,则
•
的最大值为
| BQ |
| CP |
-
| 22 |
| 9 |
-
.| 22 |
| 9 |
分析:通过建立直角坐标系,利用直线的方程联立即可得出点P,Q的坐标,再利用数量积运算和函数的单调性即可得出.
解答:解:如图所示,建立直角坐标系.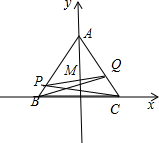 则A(0,
则A(0,
),B(-1,0),C(1,0),M(0,
).
设直线l的斜率为k,则(-
≤k≤
).则直线l的方程为y=kx+
.
又直线AC的方程为x+
=1,直线AB的方程为-x+
=1.
联立
,解得Q(
,
).
同理解得P(
,
).
∴
•
=(
+1,
)•(
-1,
)=
=2+
,
∵0≤k2≤
.
∴当且仅当k=0时,
•
的最大值为 -
.
故答案为-
.
 则A(0,
则A(0,| 3 |
| ||
| 3 |
设直线l的斜率为k,则(-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
又直线AC的方程为x+
| y | ||
|
| y | ||
|
联立
|
| 2 | ||
3+
|
1+
| ||
|
同理解得P(
| 2 | ||
|
| ||
k-
|
∴
| BQ |
| CP |
| 2 | ||
3+
|
1+
| ||
|
| 2 | ||
|
| ||
k-
|
| 6k2+22 |
| 3k2-9 |
| 40 |
| 3k2-9 |
∵0≤k2≤
| 1 |
| 3 |
∴当且仅当k=0时,
| BQ |
| CP |
| 22 |
| 9 |
故答案为-
| 22 |
| 9 |
点评:通过建立直角坐标系利用直线的方程联立得出交点坐标及掌握数量积运算和函数的单调性等是解题的关键.

练习册系列答案
相关题目
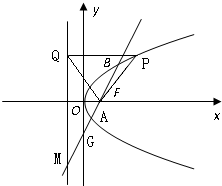 如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.
如图,已知抛物线y2=2px(p>0),焦点为F,准线为直线l,P为抛物线上的一点,过点P作l的垂线,垂足为点Q.当P的横坐标为3时,△PQF为等边三角形.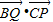 的最大值为 .
的最大值为 .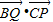 的最大值为 .
的最大值为 .