题目内容
已知奇函数f(x)=
|
(1)求实数m的值,并在给出的直角坐标系中画出y=f(x)的图象.
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试确定a的取值范围.
分析:(1)由奇函数f(x)=
的定义,对应相等求出m的值;画出图象.
(2)根据函数的图象知函数的单调递增区间,从而得到|a|-2的一个不等式,解不等式就求得a 的取值范围.
|
(2)根据函数的图象知函数的单调递增区间,从而得到|a|-2的一个不等式,解不等式就求得a 的取值范围.
解答: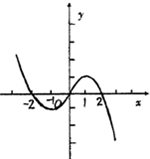 解:(1)当x<0时,-x>0,f(-x)=-(x)2+2(-x)=-x2-2x
解:(1)当x<0时,-x>0,f(-x)=-(x)2+2(-x)=-x2-2x
又f(x)为奇函数,∴f(-x)=-f(x)=-x2-2x,∴f(x)=x2+2x,∴m=2
y=f(x)的图象如右所示
(2)由(1)知f(x)=
,
由图象可知,f(x)在[-1,1]上单调递增,要使f(x)在[-1,|a|-2]上单调递增,只需
解之得-3≤a<-1或1<a≤3
 解:(1)当x<0时,-x>0,f(-x)=-(x)2+2(-x)=-x2-2x
解:(1)当x<0时,-x>0,f(-x)=-(x)2+2(-x)=-x2-2x又f(x)为奇函数,∴f(-x)=-f(x)=-x2-2x,∴f(x)=x2+2x,∴m=2
y=f(x)的图象如右所示
(2)由(1)知f(x)=
|
由图象可知,f(x)在[-1,1]上单调递增,要使f(x)在[-1,|a|-2]上单调递增,只需
|
点评:考查奇函数的定义,应用转化的思想求值;作函数的图象,求a的取值范围,体现了作图和用图的能力,属中档题.

练习册系列答案
相关题目