题目内容
已知A,B,C是球面上三点,且AB=AC=4cm,∠BAC=90°,若球心O到平面ABC的距离为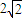 ,则该球的表面积为 cm3.
,则该球的表面积为 cm3.
【答案】分析:由已知球面上三点A、B、C满足∠BAC=90°,可得平面ABC截球所得小圆的直径等于BC长,进而求出截面圆的半径r=2 ,根据球的截面圆性质,算出球半径R=
,根据球的截面圆性质,算出球半径R= =4,代入球的表面积公式即算出该球的表面积.
=4,代入球的表面积公式即算出该球的表面积.
解答:解:∵AB=AC=4cm,∠BAC=90°,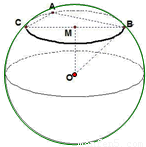
∴BC为平面ABC截球所得小圆的直径,
设小圆半径为r,得2r=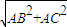 =4
=4 ,可得半径r=2
,可得半径r=2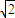
又∵球心O到平面ABC的距离d=2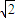
∴根据球的截面圆性质,得球半径R=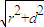 =4
=4
∴球的表面积S=4π•R2=64π
故答案为:64π
点评:本题给出球的截面圆中Rt△ABC的形状和该截面与球心的距离,求球的表面积,着重考查了球的截面圆性质、勾股定理和球的表面积公式等知识,属于基础题.
 ,根据球的截面圆性质,算出球半径R=
,根据球的截面圆性质,算出球半径R= =4,代入球的表面积公式即算出该球的表面积.
=4,代入球的表面积公式即算出该球的表面积.解答:解:∵AB=AC=4cm,∠BAC=90°,

∴BC为平面ABC截球所得小圆的直径,
设小圆半径为r,得2r=
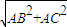 =4
=4 ,可得半径r=2
,可得半径r=2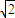
又∵球心O到平面ABC的距离d=2
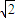
∴根据球的截面圆性质,得球半径R=
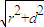 =4
=4∴球的表面积S=4π•R2=64π
故答案为:64π
点评:本题给出球的截面圆中Rt△ABC的形状和该截面与球心的距离,求球的表面积,着重考查了球的截面圆性质、勾股定理和球的表面积公式等知识,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
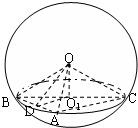 如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )
如图,已知A,B,C是表面积为48π的球面上的三点,AB=2,BC=4,∠ABC=60°,O为球心,则二面角O-AB-C的大小为:( )A、
| ||||
B、
| ||||
C、arccos
| ||||
D、arccos
|
 ,则该球的表面积为________cm3.
,则该球的表面积为________cm3.