题目内容
已知平面内一动点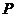 到点F(1,0)的距离与点
到点F(1,0)的距离与点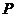 到
到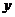 轴的距离的等等于1.
轴的距离的等等于1.
(I)求动点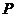 的轨迹
的轨迹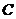 的方程;
的方程;
(II)过点 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线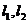 ,设
,设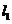 与轨迹
与轨迹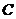 相交于点
相交于点 ,
,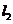 与轨迹
与轨迹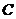 相交于点
相交于点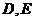 ,求
,求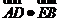 的最小值.
的最小值.
【答案】
解析:(I)设动点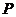 的坐标为
的坐标为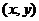 ,由题意为
,由题意为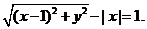
化简得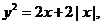
当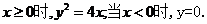 、
、
所以动点P的轨迹C的方程为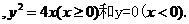
(II)由题意知,直线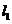 的斜率存在且不为0,设为
的斜率存在且不为0,设为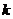 ,则
,则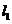 的方程为
的方程为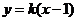 .
.
由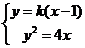 ,得
,得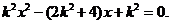
设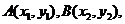 则
则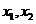 是上述方程的两个实根,于是
是上述方程的两个实根,于是
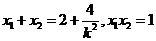 .
.
因为 ,所以
,所以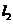 的斜率为
的斜率为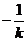 .
.
设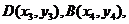 则同理可得
则同理可得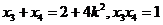
故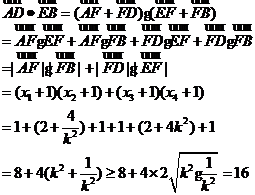
当且仅当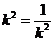 即
即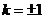 时,
时,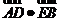 取最小值16.
取最小值16.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 到点F(1,0)的距离与点
到点F(1,0)的距离与点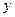 轴的距离的等等于1.
轴的距离的等等于1.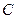 的方程;
的方程;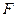 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线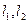 ,设
,设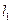 与轨迹
与轨迹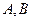 ,
,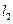 与轨迹
与轨迹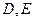 ,求
,求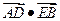 的最小值.
的最小值.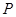 到点
到点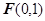 的距离与点
的距离与点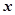 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点 的方程;(II)过点
的方程;(II)过点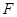 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线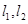 ,设
,设 与轨迹
与轨迹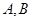 ,
,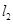 与轨迹
与轨迹 ,求
,求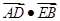 的最小值.
的最小值.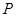 到点F(1,0)的距离与点
到点F(1,0)的距离与点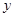 轴的距离的等等于1.
轴的距离的等等于1.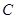 的方程;
的方程;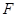 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线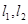 ,设
,设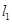 与轨迹
与轨迹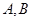 ,
,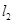 与轨迹
与轨迹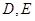 ,求
,求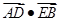 的最小值.
的最小值.