题目内容
 M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.另外只有成绩高于180分的男生才能担任“助理工作”.
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.另外只有成绩高于180分的男生才能担任“助理工作”.(I)如果用分层抽样的方法从“甲部分”人选和“乙部分”人选中选取8人,再从这8人中选3人,那么至少有一人是“甲部门”人选的概率是多少?
(II)若从所有“甲部门”人选中随机选3人,用X表示所选人员中能担任“助理工作”的人数,写出X的分布列,并求出X的数学期望.
分析:(I)由茎叶图可知甲部门、乙部门的人选数,先算出每人被抽中的概率,根据抽取比例可算出甲部门、乙部门所抽取的人数,“至少有一名甲部门人被选中”的概率等于1减去其对立事件“没有一名甲部门人被选中”的概率;
(II)依据题意,能担任“助理工作”的人数X的取值分别为0,1,2,3,通过计算即写出X的分布列,根据期望公式即可算出期望;
(II)依据题意,能担任“助理工作”的人数X的取值分别为0,1,2,3,通过计算即写出X的分布列,根据期望公式即可算出期望;
解答:解:(I)用分层抽样的方法,每个人被抽中的概率为
=
,
根据茎叶图,有“甲部门”人选10人,“乙部门”人选10人,
所以选中的“甲部门”人选有10×
=4人,“乙部门”人选有10×
=4人,
用事件A表示“至少有一名甲部门人被选中”,则它的对立事件
表示“没有一名甲部门人被选中”,则P(A)=1-P(
)=1-
=1-
=
.
因此,至少有一人是“甲部门”人选的概率是
;
(Ⅱ)依据题意,所选毕业生中能担任“助理工作”的人数X的取值分别为0,1,2,3,
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,P(X=3)=
=
.
因此,X的分布列如下:
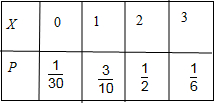
所以X的数学期望EX=0×
+1×
+2×
+3×
=
.
| 8 |
| 20 |
| 2 |
| 5 |
根据茎叶图,有“甲部门”人选10人,“乙部门”人选10人,
所以选中的“甲部门”人选有10×
| 2 |
| 5 |
| 2 |
| 5 |
用事件A表示“至少有一名甲部门人被选中”,则它的对立事件
. |
| A |
. |
| A |
| ||
|
| 4 |
| 56 |
| 13 |
| 14 |
因此,至少有一人是“甲部门”人选的概率是
| 13 |
| 14 |
(Ⅱ)依据题意,所选毕业生中能担任“助理工作”的人数X的取值分别为0,1,2,3,
P(X=0)=
| ||||
|
| 1 |
| 30 |
| ||||
|
| 3 |
| 10 |
| ||||
|
| 1 |
| 2 |
| ||||
|
| 1 |
| 6 |
因此,X的分布列如下:

所以X的数学期望EX=0×
| 1 |
| 30 |
| 9 |
| 30 |
| 15 |
| 30 |
| 5 |
| 30 |
| 9 |
| 5 |
点评:本题考查离散型随机变量的分布列、期望,考查茎叶图、分层抽样,考查学生对问题的分析理解能力,掌握相关概念、公式是解决该类问题的基础.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 (2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
 M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.