题目内容
在锐角△ABC中，角A、B、C的对边分别为a、b、c，且
（1）求角
；
（2）若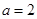
，求
面积S的最大值.
（1）
；（2）
.
解析试题分析：（1）由式子的结构特征，很自然联想到余弦定理，将其化为关于角的三角函数，由其函数值则可求出角；（2）由第（1）题的结果，可知
，再由条件可得，
，利用基本不等式可求出
的最大值，进一步可得三角形面积的最大值.
试题解析：
（1）由已知得
，所以
，
又在锐角中，所以
（2）因为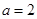，，所以
而
又
所以面积
的最大值等于
考点：余弦定理、三角形面积、基本不等式.
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
，
，
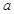分别是
的三个内角
，
，
所对的边，若
，
，
，求边
．
的最小值和最小正周期；
内角
的对边分别为
，且
，若向量
与
共线，求
的值．
ABC中，内角A，B，C的对边分别为a，b，c．
，
.
的值； (Ⅱ)若
，求
中，
分别为角
的对边，△ABC的面积S满足
.
的值；
，设角
的大小为
用
表示
，并求
的内角
所对边的长分别为
，且有
．
，
，
为
的中点，求
的长．
中，
，
，
分别是角
，
，
的对边，向量
，
，且
//
．
的大小；
，且
的最小正周期为
，求
上的最大值和最小值．
中，角
的对边分别为
，已知
.
的值；
，求
和
的值.
中，已知
；
，
，求
.