题目内容
3.已知函数f(x)=-x2+x,g(x)=$\left\{\begin{array}{l}{f(x),x≤a}\\{f(x-1)-1,x>a}\end{array}\right.$,若关于x的方程g(x)=t对任意的t<$\frac{1}{4}$都恰有两个不同的解,则实数a的取值集合是{$\frac{3}{2}$}.分析 求出g(x)的解析式,画出图象,讨论a>$\frac{3}{2}$时,a<$\frac{3}{2}$时,a=$\frac{3}{2}$时,分段函数的图象的特点,根据题意结合图象即可得到所求a的取值集合.
解答 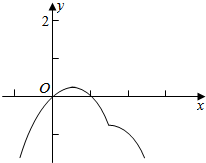 解:g(x)=$\left\{\begin{array}{l}{x-{x}^{2},x≤a}\\{(x-1)-(x-1)^{2}-1,x>a}\end{array}\right.$
解:g(x)=$\left\{\begin{array}{l}{x-{x}^{2},x≤a}\\{(x-1)-(x-1)^{2}-1,x>a}\end{array}\right.$
=$\left\{\begin{array}{l}{x-{x}^{2},x≤a}\\{3x-3-{x}^{2},x>a}\end{array}\right.$,
作出g(x)的图象,
当x≤a时,g(x)的对称轴x=$\frac{1}{2}$,顶点为($\frac{1}{2}$,$\frac{1}{4}$).
当x>a时,g(x)的对称轴为x=$\frac{3}{2}$,
由(a-1)-(a-1)2-1=a-a2,解得a=$\frac{3}{2}$.
当a>$\frac{3}{2}$时,x>a时,函数递减,x≤a,g(x)不单调,
x=a时,(a-1)-(a-1)2-1>a-a2,
关于x的方程g(x)=t对任意的t<$\frac{1}{4}$不都有两个不同的解;
当a<$\frac{3}{2}$时,x>a和x≤a中,g(x)总有一个不单调,
且x=a时,(a-1)-(a-1)2-1<a-a2,
关于x的方程g(x)=t对任意的t<$\frac{1}{4}$不都有两个不同的解;
故只有a=$\frac{3}{2}$时,关于x的方程g(x)=t对任意的t<$\frac{1}{4}$恰有两个不同的解.
故答案为:{$\frac{3}{2}$}.
点评 本题考查函数和方程的转化思想,考查函数的性质的运用,考查分类讨论和数形结合的思想方法,属于中档题.

| A. | 前后相对侧面 | B. | 上下相对底面 | C. | 左右相对侧面 | D. | 相邻的侧面 |