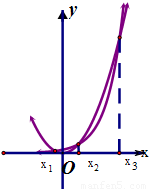
题目内容
 函数y=2x-2和y=
函数y=2x-2和y=| 1 |
| 3 |
(Ⅰ)请指出图中曲线C1、C2分别对应的函数;
(Ⅱ)现给下列二个结论:
①当x∈(-∞,-1)时,2x-2<
| 1 |
| 3 |
②x2∈(1,2);
请你判定是否成立,并说明理由.
分析:(I)根据已知中两个函数的图象,结合二次函数在对称轴左右两侧单调性相反,而指数函数在定义上单调,可分析出图中曲线C1、C2分别对应的函数;
(Ⅱ)①由函数解析式可得当x=-1时,两函数的函数值相等,结合两个函数在区间(-∞,-1)上的单调性,可得结论;②构造函数f(x)=2x-2-
x2,根据函数零点存在定理可判断其真假.
(Ⅱ)①由函数解析式可得当x=-1时,两函数的函数值相等,结合两个函数在区间(-∞,-1)上的单调性,可得结论;②构造函数f(x)=2x-2-
| 1 |
| 3 |
解答:解:(Ⅰ)由已知中曲线C1有一段从左到右是下降的
故C1为y=
x2,…(3分)
则C2为y=2x-2; …(5分)
(Ⅱ)结论①成立,理由如下:
∵函数y=2x-2在(-∞,-1]上是增函数,
∴x∈(-∞,-1)时,2x-2<2-1-2=
.…(7分)
又∵函数y=
x2在(-∞,-1]上是减函数,
∴x∈(-∞,-1)时,
x2>
×(-1)2=
而
<
,
所以当x∈(-∞,-1)时,2x-2<
x2;…(10分)
结论②成立,理由如下:
构造函数f(x)=2x-2-
x2,
则f(1)=
>0,f(2)=-
<0
∴f(x)在区间(1,2)内有零点.…(14分)
故C1为y=
| 1 |
| 3 |
则C2为y=2x-2; …(5分)
(Ⅱ)结论①成立,理由如下:
∵函数y=2x-2在(-∞,-1]上是增函数,
∴x∈(-∞,-1)时,2x-2<2-1-2=
| 1 |
| 8 |
又∵函数y=
| 1 |
| 3 |
∴x∈(-∞,-1)时,
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 3 |
所以当x∈(-∞,-1)时,2x-2<
| 1 |
| 3 |
结论②成立,理由如下:
构造函数f(x)=2x-2-
| 1 |
| 3 |
则f(1)=
| 1 |
| 6 |
| 1 |
| 3 |
∴f(x)在区间(1,2)内有零点.…(14分)
点评:本题考查的知识点是函数的图象和性质,函数与不等式之间的辩证关系,函数的零点,熟练掌握二次函数及指数函数的图象和性质是解答的关键.

练习册系列答案
相关题目
 函数y=2x-2和y=
函数y=2x-2和y=
 x2的图象如图所示,其中有且只有X=x1,x2,x3时,两函数值相等,
x2的图象如图所示,其中有且只有X=x1,x2,x3时,两函数值相等,
 x2的图象如图所示,其中有且只有X=x1,x2,x3时,两函数值相等,
x2的图象如图所示,其中有且只有X=x1,x2,x3时,两函数值相等,