Question

函数y=2^x-2和y=

1

3

x²的图象如图所示，其中有且只有X=x₁，x₂，x₃时，两函数值相等，
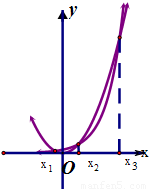
且x₁＜0＜x₂＜x₃，0为坐标原点．现给出下列三个结论：
①当x∈（-∞，-1）时，2^x-2＜x²；
②x₂∈（1，2）；
③x₃∈（4，5）．其中正确结论的序号为

①②

．

Answer 1

分析：先将函数图象交点范围问题转化为函数f（x）=2^x-2-

1

3

x²的零点问题，再利用零点存在性定理，判断零点范围即可作出正确选择

解答：解：设函数f（x）=2^x-2-

1

3

x²，
∵f（-1）=

1

8

-

1

3

＜0，f（0）=

1

4

＞0
∴f（x）的一个零点在（-1，0）上，即-1＜x₁＜0，①正确；
∵f（1）=

1

2

-

1

3

＞0，f（2）=1-

4

3

＜0
∴1＜x₂＜2，②正确
同理，f（4）=4-

16

3

＜0，f（5）=8-

25

3

＜0，f（6）=16-

36

3

＞0
∴5＜x₃＜6，③错误
故答案为①②

点评：本题主要考查了函数零点的存在性定理和零点范围的判断方法，函数零点问题与函数图象交点问题间的联系和相互转化，一定的运算能力和比较大小能力