题目内容
已知⊙C过点P(1,1),且与⊙M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求
•
的最小值.
(1)求⊙C的方程;
(2)设Q为⊙C上的一个动点,求
| PQ |
| MQ |
分析:(1)设圆心的坐标,利用对称的特征,建立方程组,从而求出圆心坐标,又⊙C过点P(1,1),可得半径,故可写出⊙C方程.
(2)设Q的坐标,用坐标表示两个向量的数量积,化简后再进行三角代换,可得其最小值.
(2)设Q的坐标,用坐标表示两个向量的数量积,化简后再进行三角代换,可得其最小值.
解答:解:(1)设圆心C(a,b),则
,解得 a=0,b=0
则圆C的方程为x2+y2=r2,
将点P的坐标(1,1)代入得r2=2,
故圆C的方程为x2+y2=2;
(2)设Q(x,y),则x2+y2=2,
•
=(x-1,y-1)•(x+2,y+2)=x2+y2+x+y-4=x+y-2,
令x=
cosθ,y=
sinθ,
∴
•
=
cosθ+
sinθ-2=2sin(θ+
)-2,
∴θ+
=2kπ-
时,sin(θ+
)的最小值为-1,
所以
•
的最小值为-2-2=-4.
|
则圆C的方程为x2+y2=r2,
将点P的坐标(1,1)代入得r2=2,
故圆C的方程为x2+y2=2;
(2)设Q(x,y),则x2+y2=2,
| PQ |
| MQ |
令x=
| 2 |
| 2 |
∴
| PQ |
| MQ |
| 2 |
| 2 |
| π |
| 4 |
∴θ+
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
所以
| PQ |
| MQ |
点评:本题考查圆的对称性,考查圆的标准方程,考查两个向量的数量积公式的应用,直线与圆的位置关系的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
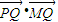 的最小值;
的最小值;