题目内容
如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是底面边长的
倍，P为侧棱SD上的点．
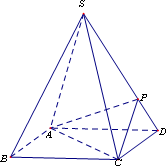
(1)求证：AC⊥面SBD；
(2)若SD⊥平面PAC，求二面角P―AC―D的大小
(3)在(2)的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE∶EC的值；若不存在，试说明理由．
答案：
解析：
解析：
|
解：(1)(4分)连BD，设AC交BD于O，由题意 (2)(4分)设正方形边长 又 连 且 由 即二面角 (3)(4分)在棱SC上存在一点E，使 由(2)可得 |
．在正方形ABCD中，
，所以
．
，则
．
，所以
，由(Ⅰ)知
，所以
，
，所以
是二面角
的平面角．
，知
，所以
，
的大小为
．
，故可在
上取一点
，使
，过
作
的平行线与
的交点即为
．连BN．在△BDN中知
，又由于
，故平面
，得
，由于
，故
．
练习册系列答案
相关题目
如图，四棱锥S-ABCD中，SD⊥底面ABCD，AB∥DC，AD⊥DC，AB=AD=1，DC=SD=2，E为棱SB上的一点，平面EDC⊥平面SBC．
如图，四棱锥S-ABCD的底面是边长为3的正方形，SD丄底面ABCD，SB=
（2013•醴陵市模拟）如图，四棱锥S-ABCD的底面是矩形，SA⊥底面ABCD，P为BC边的中点，AD=2，AB=1．SP与平面ABCD所成角为
如图，四棱锥S-ABCD底面ABCD是正方形，SA⊥底面ABCD，E是SC上一点，且SE=2EC，SA=6，AB=2．
（2006•西城区二模）如图，四棱锥S-ABCD中，平面SAC与底面ABCD垂直，侧棱SA、SB、SC与底面ABCD所成的角均为45°，AD∥BC，且AB=BC=2AD．