题目内容
 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(1)证明平面BG∥平面SDE;
(2)求面SAD与面SBC所成二面角的大小.
分析:(1)在SD上取点F,使SF=
SD,连接FG、FE,根据比例关系可得BG∥FE,而FE⊆平面SDE,BG?平面SDE,满足线面平行的判定度量所需条件;
(2)连接BD,设面SAD与面ABC所成二面角的平面角为θ,根据面积射影法cosθ=
=
求出二面角的平面角的余弦值即可.
| 2 |
| 3 |
(2)连接BD,设面SAD与面ABC所成二面角的平面角为θ,根据面积射影法cosθ=
| S△SAD |
| S△SBC |
| ||
|
解答:解:(1)在SD上取点F,使SF=
SD,连接FG、FE,由CG=
SC得FG
CD,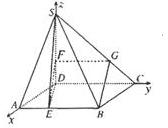
又AE=
AB得BE
CD,∴FG
BE,∴BG∥FE
∵FE⊆平面SDE,BG?平面SDE
∴BG∥平面SDE.
(2)连接BD,在正方形ABCD中,BC=3,∴BD=3
,∵SD⊥面ABCD,∴SD⊥BD,又SB=3
,∴SD=3,
又面SAD⊥面ABCD,面SCD⊥面ABCD,∴BC⊥SC,BA⊥面SAD,CD⊥面SAD,
设面SAD与面ABC所成二面角的平面角为θ,则
cosθ=
=
=
=
∴θ=
,即面ASD与面BSC所成二面角的大小为
.
| 2 |
| 3 |
| 1 |
| 3 |
| ∥ |
. |
| 2 |
| 3 |

又AE=
| 1 |
| 3 |
| ∥ |
. |
| 2 |
| 3 |
| ∥ |
. |
∵FE⊆平面SDE,BG?平面SDE
∴BG∥平面SDE.
(2)连接BD,在正方形ABCD中,BC=3,∴BD=3
| 2 |
| 3 |
又面SAD⊥面ABCD,面SCD⊥面ABCD,∴BC⊥SC,BA⊥面SAD,CD⊥面SAD,
设面SAD与面ABC所成二面角的平面角为θ,则
cosθ=
| S△SAD |
| S△SBC |
| ||
|
| 3×3 | ||
3×3
|
| ||
| 2 |
∴θ=
| π |
| 4 |
| π |
| 4 |
点评:本题主要考查了线面平行的判断,以及二面角平面角的度量等有关知识,同时考查空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.