题目内容
计算下列几个式子：
①2（sin35°cos25°+sin55°cos65°），
②tan25°+tan35°+
tan25°tan35°，
③
，
④
，
⑤2cos4
-2sin4
结果为
的是
①2（sin35°cos25°+sin55°cos65°），
②tan25°+tan35°+
| 3 |
③
tan
| ||
1-tan2
|
④
| 1+tan15° |
| 1-tan15° |
⑤2cos4
| π |
| 12 |
| π |
| 12 |
结果为
| 3 |
①②④⑤
①②④⑤
（填上所有你认为正确答案的序号）分析：根据两角和差的正弦，余弦，正切公式及二倍角公式，逐一计算各式的值，可得答案．
解答：解：①2（sin35°cos25°+sin55°cos65°）=2sin（35°+25°）=2sin60°=
，
②tan25°+tan35°+
tan25°tan35°=tan60°（1-tan25°tan35°）+
tan25°tan35°=
-
tan25°tan35°+
tan25°tan35°=
，
③
=
tan
=
，
④
=
=tan60°=
，
⑤2cos4
-2sin4
=2（cos2
-sin2
）（cos2
+sin2
）=2（cos2
-sin2
）=2cos
=
，
故结果为
的是①②④⑤
故答案为：①②④⑤
| 3 |
②tan25°+tan35°+
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
③
tan
| ||
1-tan2
|
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
④
| 1+tan15° |
| 1-tan15° |
| tan45°+tan15° |
| 1-tan45°•tan15° |
| 3 |
⑤2cos4
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
| 3 |
故结果为
| 3 |
故答案为：①②④⑤
点评：本题考查的知识点两角和与差的余弦公式，两角和与差的正弦公式，两角和与差的正切公式，二倍角的余弦公式，熟练掌握上述公式是解答的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
，
， 
，
的是 （填上所有你认为正确答案的序号）
,
, 
，
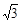的是（
）