题目内容
(Ⅰ)设f(x)是定义在实数集R上的函数,满足f(0)=1,且对任意实数a,b,有f(a-b)=f(a)-b(2a-b+1),求f(x);
(Ⅱ)函数f(x)(x∈(-1,1))满足2f(x)-f(-x)=lg(x+1),求f(x)。
(Ⅱ)函数f(x)(x∈(-1,1))满足2f(x)-f(-x)=lg(x+1),求f(x)。
解:(Ⅰ)f(a-b)=f(a)-b(2a-b+1)(a,b∈R),
令a=b=x,则f(0)=f(x)-x(2x-x+1),
又f(0)=1,
∴f(x)=x2+x+1。
(Ⅱ)用-x代替关系中的x,得2f(-x)-f(x)=lg(-x+1),
解方程组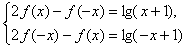 ,
,
解得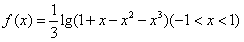 。
。
令a=b=x,则f(0)=f(x)-x(2x-x+1),
又f(0)=1,
∴f(x)=x2+x+1。
(Ⅱ)用-x代替关系中的x,得2f(-x)-f(x)=lg(-x+1),
解方程组
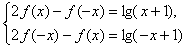 ,
,解得
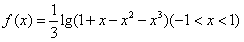 。
。
练习册系列答案
相关题目
设
f(x)是连续函数,且为偶函数,在对称区间[-a,a]上的积分 ,由定积分的几何意义和性质得
,由定积分的几何意义和性质得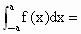
[
]|
A .0 |
B . |
|
C . |
D . |