题目内容
3.函数y=ax-5+31(a≠0)的图象过定点P,且点P在指数函数f(x)=bx的图象上,则f(2)=4.分析 根据指数函数的图象过定点(0,1),求出点P的坐标,再代入指数函数f(x)的解析式,求出f(x),从而求出f(2)的值.
解答 解:∵函数y=ax-5+31(a≠0)的图象过定点P,
令x-5=0,解得x=5,
∴y=1+31=32,
即点P(5,32);
又点P在指数函数f(x)=bx的图象上,
∴f(5)=b5=32,
解得b=2,
∴f(x)=2x;
∴f(2)=22=4.
故答案为:4.
点评 本题考查了指数函数的图象恒过定点的应用问题,是基础题目.

练习册系列答案
相关题目
11.设函数f(x)=x(ex-e-x),则使得f(x)>f(2x-1)成立的x的取值范围是( )
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
18.若函数y=ax(a>0且a≠1)在[0,1]上的最大值与最小值之和为3,则tan$\frac{a•180°}{6}$的值为( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
8.已知数列{an}为等比数列,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为$\frac{5}{4}$,则S6=( )
| A. | 35 | B. | 33 | C. | 31 | D. | $\frac{63}{2}$ |
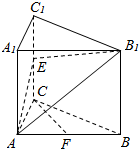 已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.
已知直棱柱ABC-A1B1C1,∠ACB=60°,AC=BC=4,AA1=6,E、F分别是棱CC1、AB的中点.