题目内容
将二项式 的展开式中所有项重新排成一列,有理式不相邻的排法有( )种.
的展开式中所有项重新排成一列,有理式不相邻的排法有( )种.
A. | B. | C. | D. |
C
解析试题分析: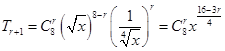 ,其中
,其中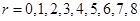
易知当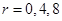 时,第
时,第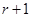 项为有理项,其它的六项为无理项;所以,将二项式
项为有理项,其它的六项为无理项;所以,将二项式 的展开式中所有项重新排成一列,第一步排无理项有
的展开式中所有项重新排成一列,第一步排无理项有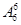 种不同的排列方法,第二步,因为六个无理项共形成7个空,从中选出3个排三个有理式,有
种不同的排列方法,第二步,因为六个无理项共形成7个空,从中选出3个排三个有理式,有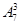 种不同的结果.所以,有理式不相邻的排法有
种不同的结果.所以,有理式不相邻的排法有 种.故选C.
种.故选C.
考点:1、二项式定理;2、排列组合.

练习册系列答案
相关题目
若(9x- )n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为( )
)n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为( )
| A.252 | B.-252 | C.84 | D.-84 |
已知 的最小值是
的最小值是 ,则二项式
,则二项式 展开式中
展开式中 项的系数为( )
项的系数为( )
A. | B. | C. | D. |
二项式 展开式中含有
展开式中含有 项,则
项,则 可能的取值是( )
可能的取值是( )
| A.5 | B.6 | C.7 | D.8 |
某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( )
| A.474种 | B.77种 | C.462种 | D.79种 |
将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有 ( )
| A. 240种 | B. 300种 | C.360种 | D.420种 |
已知集合A={1,2,3,4},B={5,6,7},C={8,9},现在从这三个集合中的两个集合中的各取出1个元素,则一共可以组成集合的个数为( )
| A.24 | B.36 | C.26 | D.27 |
 5的展开式中各项系数之和为3,则该展开式中常数项为( ).
5的展开式中各项系数之和为3,则该展开式中常数项为( ).
| A.40 | B.160 | C.0 | D.320 |