题目内容
已知直线x+ky-3=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为8.(1)求椭圆C的标准方程;
(2)已知圆O:x2+y2=1,直线l:mx+ny=1.试证明:当点P(m,n)在椭圆C上运动时,直线l与圆O恒相交,并求直线l被圆O所截得的弦长L的取值范围.
【答案】分析:(1)由x+ky-3=0得,(x-3)+ky=0,所以F为(3,0).由题设知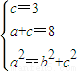 ,由此可求出椭圆C的方程.
,由此可求出椭圆C的方程.
(2)因为点P(m,n)在椭圆C上运动,所以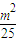 +
+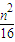 =1.从而圆心O到直线l的距离d=
=1.从而圆心O到直线l的距离d=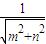 =
=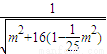 =
=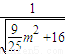 <1.由此可求出直线l被圆O截得的弦长的取值范围.
<1.由此可求出直线l被圆O截得的弦长的取值范围.
解答:解:(1)由x+ky-3=0得,(x-3)+ky=0,
所以直线过定点(3,0),即F为(3,0).
设椭圆C的方程为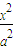 +
+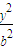 =1(a>b>0),
=1(a>b>0),
则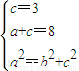 解得
解得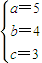
故所求椭圆C的方程为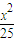 +
+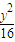 =1.
=1.
(2)因为点P(m,n)在椭圆C上运动,所以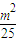 +
+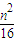 =1.
=1.
从而圆心O到直线l的距离
d=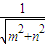 =
=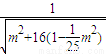 =
=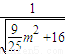 <1.
<1.
所以直线l与圆O恒相交.
又直线l被圆O截得的弦长
L=2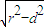 =2
=2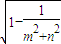 =2
=2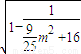 ,由于0≤m2≤25,
,由于0≤m2≤25,
所以16≤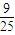 m2+16≤25,则L∈[
m2+16≤25,则L∈[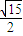 ,
,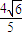 ],
],
即直线l被圆O截得的弦长的取值范围是[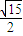 ,
,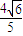 ].
].
点评:本题考查直线和圆的综合应用,解题时要认真审题,掌握椭圆方程的求解方法,注意弦长公式的合理运用.
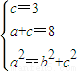 ,由此可求出椭圆C的方程.
,由此可求出椭圆C的方程.(2)因为点P(m,n)在椭圆C上运动,所以
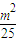 +
+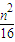 =1.从而圆心O到直线l的距离d=
=1.从而圆心O到直线l的距离d=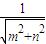 =
=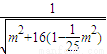 =
=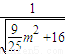 <1.由此可求出直线l被圆O截得的弦长的取值范围.
<1.由此可求出直线l被圆O截得的弦长的取值范围.解答:解:(1)由x+ky-3=0得,(x-3)+ky=0,
所以直线过定点(3,0),即F为(3,0).
设椭圆C的方程为
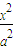 +
+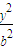 =1(a>b>0),
=1(a>b>0),则
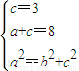 解得
解得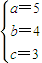
故所求椭圆C的方程为
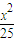 +
+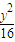 =1.
=1.(2)因为点P(m,n)在椭圆C上运动,所以
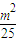 +
+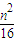 =1.
=1.从而圆心O到直线l的距离
d=
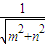 =
=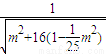 =
=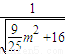 <1.
<1.所以直线l与圆O恒相交.
又直线l被圆O截得的弦长
L=2
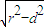 =2
=2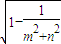 =2
=2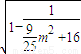 ,由于0≤m2≤25,
,由于0≤m2≤25,所以16≤
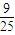 m2+16≤25,则L∈[
m2+16≤25,则L∈[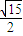 ,
,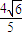 ],
],即直线l被圆O截得的弦长的取值范围是[
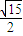 ,
,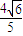 ].
].点评:本题考查直线和圆的综合应用,解题时要认真审题,掌握椭圆方程的求解方法,注意弦长公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目