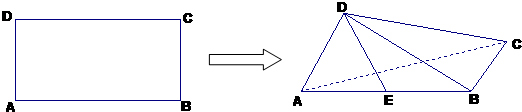
题目内容
如图,在长方形ABCD中,AB=
,BC=1,E为线段DC上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
.
| 3 |
| π |
| 3 |
| π |
| 3 |

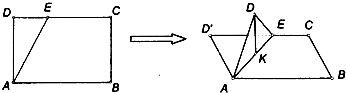
分析:根据图形的翻折过程中变与不变的量和位置关系知,若连接D'K,则D'KA=90°,得到K点的轨迹是以AD'为直径的圆上一弧,根据长方形的边长得到圆的半径,求得此弧所对的圆心角的弧度数,利用弧长公式求出轨迹长度.
解答: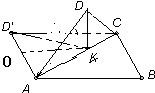 解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,
解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,
则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,根据长方形知圆半径是
,
如图当E与C重合时,AK=
=
,
取O为AD′的中点,得到△OAK是正三角形.
故∠K0A=
,∴∠K0D'=
,
其所对的弧长为
×
=
,
故答案为:
 解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,
解:由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,根据长方形知圆半径是
| 1 |
| 2 |
如图当E与C重合时,AK=
| 1×1 | ||
|
| 1 |
| 2 |
取O为AD′的中点,得到△OAK是正三角形.
故∠K0A=
| π |
| 3 |
| 2π |
| 3 |
其所对的弧长为
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查与二面角有关的立体几何综合题目,解题的关键是由题意得出点K的轨迹是圆上的一段弧,翻折问题中要注意位置关系与长度等数量的变与不变.本题是一个中档题目.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
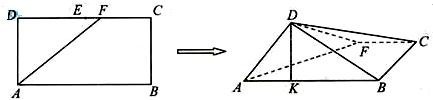
 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
若一个n面体有m个面时直角三角形,则称这个n面体的直度为 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=