题目内容
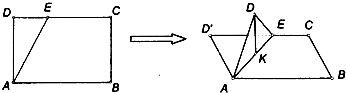
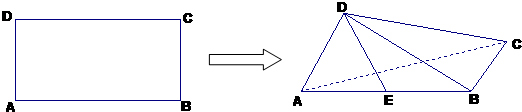
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是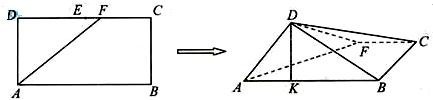
分析:此题的破解可采用二个极端位置法,即对于F位于DC的中点时与随着F点到C点时,分别求出此两个位置的t值即可得到所求的答案
解答:解:此题的破解可采用二个极端位置法,即对于F位于DC的中点时,可得t=1,
随着F点到C点时,当C与F无限接近,不妨令二者重合,此时有CD=2
因CB⊥AB,CB⊥DK,
∴CB⊥平面ADB,即有CB⊥BD,
对于CD=2,BC=1,在直角三角形CBD中,得BD=
,
又AD=1,AB=2,再由勾股定理可得∠BDA是直角,因此有AD⊥BD
再由DK⊥AB,可得三角形ADB和三角形AKD相似,可得t=
,
因此t的取值的范围是(
,1)
故答案为(
,1)
随着F点到C点时,当C与F无限接近,不妨令二者重合,此时有CD=2
因CB⊥AB,CB⊥DK,
∴CB⊥平面ADB,即有CB⊥BD,
对于CD=2,BC=1,在直角三角形CBD中,得BD=
| 3 |
又AD=1,AB=2,再由勾股定理可得∠BDA是直角,因此有AD⊥BD
再由DK⊥AB,可得三角形ADB和三角形AKD相似,可得t=
| 1 |
| 2 |
因此t的取值的范围是(
| 1 |
| 2 |
故答案为(
| 1 |
| 2 |
点评:考查空间图形的想象能力,及根据相关的定理对图形中的位置关系进行精准判断的能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
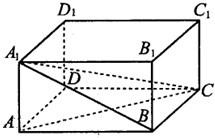 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
若一个n面体有m个面时直角三角形,则称这个n面体的直度为 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=