题目内容
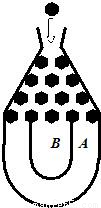
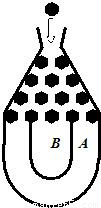
某超市为促销商品,特举办“购物有奖100%中奖”活动,凡消费者在该超市购物满100元,享受一次摇奖机会,购物满200元,享受两次摇奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落。小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为20元,落入B袋为二等奖,奖金为10元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是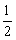 。
。
(Ⅰ)求:摇奖两次,均获得一等奖的概率;
(Ⅱ)某消费者购物满200元,摇奖后所得奖金为X元,试求X的分布列与期望;
(Ⅲ)若超市同时举行购物八八折让利于消费者活动(打折后不再享受摇奖),某消费者刚好消费200元,请问他是选择摇奖还是选择打折比较划算。
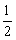 。
。(Ⅰ)求:摇奖两次,均获得一等奖的概率;
(Ⅱ)某消费者购物满200元,摇奖后所得奖金为X元,试求X的分布列与期望;
(Ⅲ)若超市同时举行购物八八折让利于消费者活动(打折后不再享受摇奖),某消费者刚好消费200元,请问他是选择摇奖还是选择打折比较划算。

| 解:记“小球落入A袋中”为事件A,“小球落入B袋中”为事件B, 则小球落入A袋中当且仅当小球一直向左落下或一直向右落下, 故 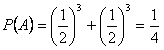 , ,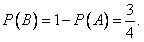 , ,(Ⅰ)获得两次一等奖的概率为  ; ;(Ⅱ)X可以取20,30,40, P(X=20)= 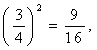 ,P(X=30)= ,P(X=30)= , ,P(X=40)=  , ,所以,分布列为:
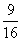 +30× +30×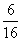 +40× +40×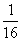 =25。 =25。 (Ⅲ)参加摇奖,可节省25元,打折优惠,可节省24元,参加摇奖。 |

练习册系列答案
相关题目
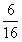
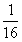
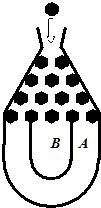 某超市为促销商品,特举办“购物有奖100%中奖”活动.凡消费者在该超市购物满10元,享受一次摇奖机会,购物满20元,享受两次摇奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落、小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为2元,落入B袋为二等奖,奖金为1元、已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是
某超市为促销商品,特举办“购物有奖100%中奖”活动.凡消费者在该超市购物满10元,享受一次摇奖机会,购物满20元,享受两次摇奖机会,以此类推.摇奖机的结构如图所示,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落、小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金为2元,落入B袋为二等奖,奖金为1元、已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是 .
.
 .
.
 .
.