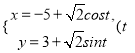题目内容
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求![]() ,并求
,并求![]() 的单调区间;
的单调区间;
(2)证明:当![]() ,
,![]() 时,
时,![]() .
.
【答案】(1)![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析.
上单调递减;(2)证明见解析.
【解析】
(1)根据极值点可求出![]() ,根据导函数的正负求出单调区间;
,根据导函数的正负求出单调区间;
(2)法一,由函数单调性可得![]() 变形可得
变形可得![]() ,利用不等式的性质可放缩得到
,利用不等式的性质可放缩得到![]() ,构造函数
,构造函数![]() 可利用导数求最小值为0,即可得证;法二由函数单调性可得
可利用导数求最小值为0,即可得证;法二由函数单调性可得![]() 变形可得
变形可得![]() ,由不等式性质可得
,由不等式性质可得![]() ,令
,令![]() ,由导数可求出
,由导数可求出![]() 即可得证.
即可得证.
(1)![]() ,由
,由![]() 是极值点得
是极值点得![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 的单调递增区间为
的单调递增区间为![]() ;
;
由![]() 得
得![]() ,∴
,∴![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)法一:由(1)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,即
,即![]() ,故
,故![]() .
.
∴![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∵![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() 在
在![]() 处取等号,
处取等号,
∴![]() ,
,
由于取等条件不同,∴![]() .
.
法二:由(1)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,即
,即![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
令![]() ,
,![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() ,
,
由于取等条件不同,故![]() ,整理得
,整理得![]() .
.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: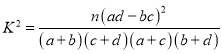 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |