题目内容
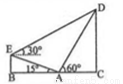
某中学举行升旗仪式，在坡度为15°的看台
点和看台的坡脚
点，分别测得旗杆顶部的仰角分别为30°和60°，量的看台坡脚
点到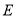
点在水平线上的射影
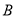点的距离为
，则旗杆的高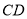
的长是__________
．
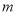练习册系列答案
小学课时特训系列答案
相关题目
小学课时特训系列答案题目内容
某中学举行升旗仪式，在坡度为15°的看台点和看台的坡脚点，分别测得旗杆顶部的仰角分别为30°和60°，量的看台坡脚点到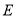点在水平线上的射影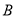点的距离为，则旗杆的高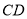的长是__________．
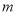小学课时特训系列答案
是定义在
上的偶函数，且对任意的
，都有
，已知当
时，
，有以下结论：
的一个周期；
在
上单调递减，在
上单调递增；
的最大值是1，最小值是0；
时，
．
，其中
且
．
的单调区间；
时，若存在
，使
成立，求实数
的取值范围．
B．
D．
，离心率为
，两焦点分别为
，过
的直线交椭圆
于
两点，且
的周长为8.
的方程；
作圆
的切线
交椭圆
于
两点，求弦长
的最大值．
，那么
的值为
B. 
C. 
D. 
,若存在实数
，使得
成立，则实数
的取值范围是_________.
，则
__________．