题目内容
如图所示,在棱长为1的正方体ABCD—A1B(1)求证:EF⊥B
(2)求EF与C
(3)求FH的长.
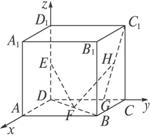
解析:如图建立空间直角坐标系D—xyz,

则E(0,0, ![]() ),F(
),F(![]() ,
,![]() ,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0,
,0),C(0,1,0),C1(0,1,1),B1(1,1,1),G(0, ![]() ,0).
,0).
(1)![]() =(
=(![]() ,
,![]() ,0)-(0,0,
,0)-(0,0, ![]() )=(
)=(![]() ,
,![]() ,-
,-![]() ),
),
![]() =(0,1,0)-(1,1,1)=(-1,0,-1).
=(0,1,0)-(1,1,1)=(-1,0,-1).
![]() ·
·![]() =(
=(![]() ,
,![]() ,-
,-![]() )(-1,0,-1)=0.
)(-1,0,-1)=0.
∴![]() ⊥
⊥![]() .∴EF⊥B
.∴EF⊥B
(2)![]() =(0,
=(0,![]() ,0)-(0,1,1)=(0,-
,0)-(0,1,1)=(0,-![]() ,-1),
,-1),
|![]() |=
|=![]() .
.
由(1)得|![]() |=
|=![]() 且
且![]() ·
·![]() =
=![]() .
.
∴cos〈![]() ,
,![]() 〉=
〉=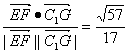 .
.
(3)∵H是![]() 的中点,H(
的中点,H(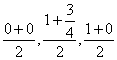 ),即(0,
),即(0,![]() ,
,![]() ),又F(
),又F(![]() ,
,![]() ,0),
,0),
∴FH=|![]() |=
|=![]() .
.

练习册系列答案
相关题目
 如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为 一点
一点 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则
 B.
B. C.
C. D.
D.
 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 取得最小值,则此最小值为
取得最小值,则此最小值为 
 的面
的面 上存在一点
上存在一点 使得
使得 取得最小值,则此
取得最小值,则此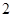 B.
B. C.
C. D.
D.