题目内容
 如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为
如图所示,在棱长为1的正方体ABCD-A1B1C1D1的面对角线A1B上存在一点P使得AP+D1P取得最小值,则此最小值为2+
|
2+
|
分析:把对角面A1C绕A1B旋转,使其与△AA1B在同一平面上,连接AD1并求出,根据平面内两点之间线段最短,可知就是最小值.
解答:解:把对角面A1C绕A1B旋转,使其与△AA1B在同一平面上,连接AD1,
则在△AA1D中,AD1=
=
为所求的最小值.
故答案为
.
则在△AA1D中,AD1=
| 1+1-2×1×1×cos135° |
2+
|
故答案为
2+
|
点评:本题的考点是点、线、面间的距离计算,主要考查考查棱柱的结构特征,考查平面内两点之间线段,最短考查计算能力,空间想象能力,是基础题.

练习册系列答案
相关题目
 一点
一点 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则
 B.
B. C.
C. D.
D.
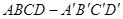 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 取得最小值,则此最小值为
取得最小值,则此最小值为 
 的面
的面 上存在一点
上存在一点 使得
使得 取得最小值,则此
取得最小值,则此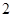 B.
B. C.
C. D.
D.