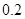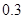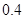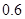题目内容
由于某高中建设了新校区,为了交通方便要用三辆通勤车从老校区把教师接到新校区.已知从新校区到老校区有两条公路,汽车走一号公路堵车的概率为
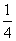 ,不堵车的概率为
,不堵车的概率为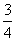 ;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.
;汽车走二号公路堵车的概率为p,不堵车的概率为1-p,若甲、乙两辆汽车走一号公路,丙汽车由于其他原因走二号公路,且三辆车是否堵车相互之间没有影响.(Ⅰ)若三辆汽车中恰有一辆汽车被堵的概率为
 ,求走二号公路堵车的概率;
,求走二号公路堵车的概率;(Ⅱ)在(Ⅰ)的条件下,求三辆汽车中被堵车辆的个数ξ的分布列和数学期望.
(1)
(2)分布列为
所以E(ξ)=0× +1×
+1× +2×
+2×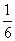 +3×
+3× =
=

(2)分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  |  | 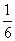 |  |
 +1×
+1× +2×
+2×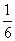 +3×
+3× =
=
试题分析:解:(Ⅰ) 由已知条件得C
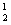 ·
·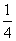 ·
·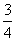 ·(1-p)+(
·(1-p)+(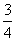 )2·p=
)2·p= , 3分
, 3分即3p=1,则p=
 ,
,即走二号公路堵车的概率为
 . 5分
. 5分(Ⅱ) ξ可能的取值为0,1,2,3,P(ξ=0)=
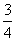 ×
×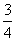 ×
× =
= ,
,P(ξ=1)=C
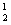 ×
×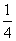 ×
×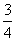 ×
× +
+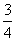 ×
×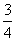 ×
× =
= ,
,P(ξ=2)=
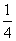 ×
×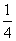 ×
× +C×
+C×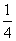 ×
×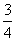 ×
× =
= ,
,P(ξ=3)=
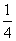 ×
×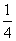 ×
× =
= .
.ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |  |  | 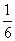 |  |
所以E(ξ)=0×
 +1×
+1× +2×
+2×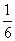 +3×
+3× =
= . 13分
. 13分点评:主要是考查了分布列和独立重复试验的概率的运用,属于中档题。

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
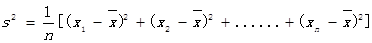 ,其中
,其中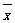 为x1,x2, ,xn的平均数)
为x1,x2, ,xn的平均数)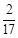
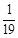
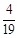
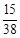
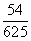
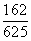
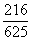
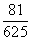
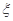 ~
~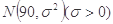 ,统计结果显示
,统计结果显示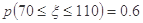 ,则
,则 ( )
( )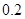
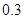
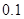
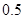
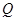 (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当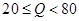 时,为酒后驾车;当
时,为酒后驾车;当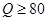 时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).
时,为醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了200辆机动车驾驶员的血酒含量(如下表).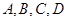 表示,醉酒驾车的人用小写字母如
表示,醉酒驾车的人用小写字母如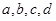 表示)
表示) 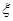 服从正态分布
服从正态分布 .若
.若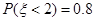 ,则
,则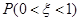 的值为( )
的值为( )