题目内容
如图所示，过定点A（a,b）任作互相垂直的两直线l1与l2,且l1与x轴交于M点，l2与y轴交于N点，求线段MN中点P的轨迹方程.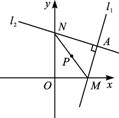
解析：设P（x,y）,M(x1,0),N(0,y1),
则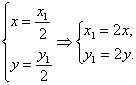
∵l1⊥l2，
∴（x1-a）2+b2+(y1-b)2+a2=x12+y12,化简得ax1+by1-a2-b2=0,
∴所求点P的轨迹方程为2ax+2by-a2-b2=0.
练习册系列答案
相关题目
题目内容
如图所示，过定点A（a,b）任作互相垂直的两直线l1与l2,且l1与x轴交于M点，l2与y轴交于N点，求线段MN中点P的轨迹方程.
解析：设P（x,y）,M(x1,0),N(0,y1),
则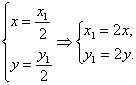
∵l1⊥l2，
∴（x1-a）2+b2+(y1-b)2+a2=x12+y12,化简得ax1+by1-a2-b2=0,
∴所求点P的轨迹方程为2ax+2by-a2-b2=0.
如图所示，已知直线l的斜率为k且过点Q（-3，0），抛物线C：y2=16x，直线与抛物线l有两个不同的交点，F是抛物线的焦点，点A（4，2）为抛物线内一定点，点P为抛物线上一动点．
如图所示，已知椭圆M：
