题目内容
1.对于任意x∈R,函数f(x)=x2-2x-|x-1-a|-|x-2|+4的值非负,则实数a的最小值为( )| A. | -$\frac{11}{8}$ | B. | -5 | C. | -3 | D. | -2 |
分析 根据条件,问题可等价为:函数g(x)的图象在函数h(x)图象的上方,再结合两函数图象的位置关系,确定a的最小值.
解答 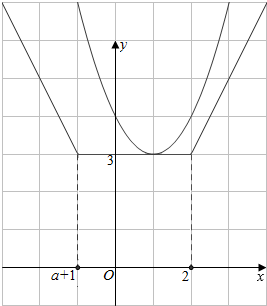 解:因为f(x)的值非负,所以f(x)≥0恒成立,
解:因为f(x)的值非负,所以f(x)≥0恒成立,
即,x2-2x+4≥|x-2|+|x-(a+1)|对任意实数x恒成立,
记g(x)=x2-2x+4,h(x)=|x-2|+|x-(a+1)|,
问题等价为:函数g(x)的图象在函数h(x)图象的上方,
其中,g(x)=(x-1)2+3,对称轴为x=1,最小值为3,
h(x)的图象的对称轴为x=$\frac{a+3}{2}$,
且函数的最小值为|(a+1)-2|=|a-1|,
由|a-1|≤3,解得a∈[-2,4],
当a=-2时,h(x)=|x-2|+|x+1|,
函数的最小值恰为3,两图象相切,
如右图,红线为g(x)图象,紫线为h(x)图象,
若a<-2,则h(x)min>3,不合题意,
因此,实数a的最小值为-2.
故选:D.
点评 本题主要考查了函数的图象和最值,涉及函数的最值,单调性和图象的对称性,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.函数f(x)=x2-2x∈{-2,-1,0,1}的值域是( )
| A. | {2,-1,-2} | B. | {2,-1,-2,-1} | C. | {4,1,0,-1} | D. | [2,-1,-2] |
12.已知$\overrightarrow{AB}=({2,1})$,$\overrightarrow{CD}=({5,5})$,则$\overrightarrow{AB}$在$\overrightarrow{CD}$方向上的投影为( )
| A. | $\frac{{-3\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{15}}}{2}$ | D. | $\frac{{-3\sqrt{15}}}{2}$ |
