题目内容
集合A={1,2,3,4,5},B={0,1,2,3,4},点P的坐标为(m,n),m∈A,n∈B,则点P在直线x+y=5下方的概率为分析:本题考查的知识点是古典概型,我们根据题意计算出基本事件总数,再计算出满足条件点P在直线x+y=5下方的基本事件个数,代入古典概型公式,即可得到答案.
解答:解:由题意知本题是古典概型问题,
基本事件总数为25,
点P在直线x+y=5下方的事件为10,
则点P在直线x+y=5下方的概率为
.
故答案为:
基本事件总数为25,
点P在直线x+y=5下方的事件为10,
则点P在直线x+y=5下方的概率为
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
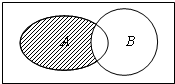 (2012•汕头一模)已知全集U=R,集合A={1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合为( )
(2012•汕头一模)已知全集U=R,集合A={1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合为( )