题目内容
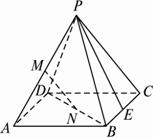
如图,已知底面是正方形且侧棱垂直于底面的四棱柱ABCD—A1B1C1D1中,底面边长为2
(1)求证:平面B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离.
(1)证明:建立如图所示的空间直角坐标系,则D(0,0,0),B(2![]() ,2
,2![]() ,0),E(2
,0),E(2![]() ,
,![]() ,0),F(
,0),F(![]() ,2
,2![]() ,0),D1(0,0,4),B1(2
,0),D1(0,0,4),B1(2![]() ,2
,2![]() ,4),
,4),

![]() =(-
=(-![]() ,
,![]() ,0),
,0),![]() =(2
=(2![]() ,2
,2![]() ,0),
,0),![]() =(0,0,4).
=(0,0,4).
∴![]()
∴EF⊥DB,EF⊥DD1.∴EF⊥平面BDD1B1.
∴平面B1EF⊥平面BDD1B1.
(2)解:设平面B1EF的法向量为n=(x,y,z),
则n⊥EF,n⊥EB1.
又![]() =(0,
=(0,![]() ,4),
,4),
∴n·![]() =-
=-![]() x+
x+![]() y=0,
y=0,
n·![]() =
=![]() y+4z=0.
y+4z=0.
∴x=y,z=-![]() y.
y.
取y=1,得n=(1,1,-![]() ).
).
又![]() ,
,
∴点D1到平面B1EF的距离为![]()

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
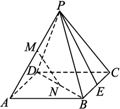
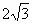 ,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.
,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.