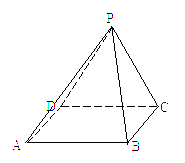题目内容
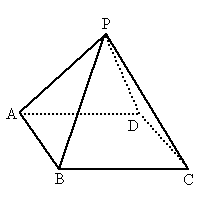
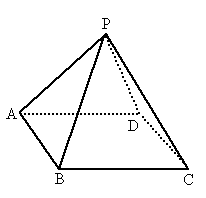
如图,底面是正方形,顶点在底面的射影是底面正方形的中心,且侧棱都相等的四棱锥,侧棱长为 ,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.
,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.
答案:略
解析:
解析:
|
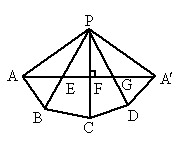
将此四棱锥 P——ABCD沿PA剪开,再将它侧面展开,连接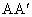 ,交PB、PC、PD于E、F、G点,然后再将此四棱锥的展开图形还原,则甲虫应按A→E→F→G→ ,交PB、PC、PD于E、F、G点,然后再将此四棱锥的展开图形还原,则甲虫应按A→E→F→G→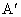 (A)的路径爬行,所经过的路程最短. (A)的路径爬行,所经过的路程最短.
∵ 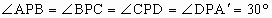 , ,
∴在 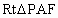 中, 中,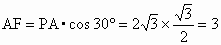
∴ 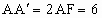 在 在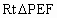 中, 中,
∴在四棱锥 P——ABCD的侧棱PB、PC、PD上分别取点E、F、G,使得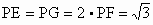 ,再连结AE、EF、FG、GA. ,再连结AE、EF、FG、GA.
∴这只甲虫应按 A→E→F→G→A的路径爬行所经过的路程最短,且最短路程为6. |

练习册系列答案
相关题目
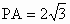
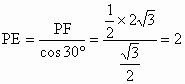
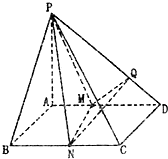 已知四棱锥P-ABCD(如图)底面是边长为2的正方形.侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD(如图)底面是边长为2的正方形.侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点,MQ⊥PD于Q. 已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.
已知四棱锥P-ABCD(如图)底面是边长为2的正方形.PA⊥平面ABCD,PA=2,M、N分别为AD、BC的中点,MQ⊥PD于Q.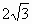 ,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.
,侧面的顶角为30°,一甲虫从A点出发绕棱锥侧面爬行一周回到A点,这只甲虫应按怎样的路径爬行,才能使它爬行的路程最短?并求最短路程.