题目内容

9、在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0），若ξ在（0，1）内的概率为0.4，则ξ在（0，2）内取值的概率为
0.8
．
分析：根据变量符合正态分布和ξ在（0，1）内的概率为0.4，由正态分布的对称性可知ξ在（1，2）内的取值概率也为0.4，根据互斥事件的概率得到要求的区间上的概率．
解答：解：∵ξ服从正态分布N（1，σ2），ξ在（0，1）内的概率为0.4，
由正态分布的对称性可知ξ在（1，2）内的取值概率也为0.4，
∴P（0＜ξ＜2）=P（0＜ξ＜1）+P（1＜ξ＜2）=0.4+0.4=0.8
故答案为：0.8
点评：本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的基本性质，考查互斥事件的概率公式，本题是一个基础题，运算量不大，不易出错．
练习册系列答案
相关题目
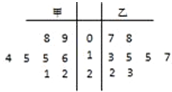精英家教网甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，
.
x
1，
.
x
2分别表示甲乙两名运动员这项测试成绩的平均数，s1，s2分别表示甲乙两名运动员这项测试成绩的标准差，则有（　　）
A、
.
x
1＞
.
x
2，s1＜s2
B、
.
x
1=
.
x
2，s1＜s2
C、
.
x
1=
.
x
2，s1=s2
D、
.
x
1＜
.
x
2，s1＞s2
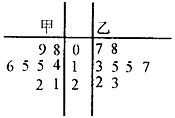精英家教网甲、乙两名运动员，在某项测试中的8次成绩如茎叶图所示，
.
x1
，
.
x2
分别表示甲、乙两名运动员这项测试成绩的平均数，s1，s2分别表示甲、乙两名运动员这项测试成绩的标准差，则有（　　）
A、
.
x1
＞
.
x2
，s1＜s2
B、
.
x1
=
.
x2
，s1＜s2
C、
.
x1
=
.
x2
，s1＞s2
D、
.
x1
＜
.
x2
，s1＞s2
（2013•临沂三模）甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，
.
x
1，
.
x
2分别表示甲乙两名运动员这项测试成绩的平均数，s1，s2分别表示甲乙两名运动员这项测试成绩的标准差，则有（　　）
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，
.
x
1，
.
x
2分别表示甲乙两名运动员这项测试成绩的平均数，s1，s2分别表示甲乙两名运动员这项测试成绩的标准差，a1，a2分别表示甲乙两名运动员这项测试成绩的中位数，则有（　　）
甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示，x1，x2分别表示甲乙两名运动员这项测试成绩的众数，y1，y2分别表示甲乙两名运动员这项测试成绩的中位数，则有（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网