题目内容
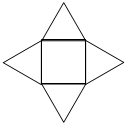 如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为
如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为分析:由已知中正四棱锥的展开图为一个边长为2的正方形及四个正三角形,我们可以分别计算出棱锥的底面面积和高,代入棱锥体积公式,即可求出折起后形成的四棱锥的体积.
解答:解:由已知中由一个边长为2的正方形及四个正三角形构成
故该棱锥的底面面积S=2×2=4
侧高为正三角形的高
则棱锥的高h=
=
故折起后形成的四棱锥的体积V=
Sh=
故答案为:
故该棱锥的底面面积S=2×2=4
侧高为正三角形的高
| 3 |
则棱锥的高h=
| 3-1 |
| 2 |
故折起后形成的四棱锥的体积V=
| 1 |
| 3 |
4
| ||
| 3 |
故答案为:
4
| ||
| 3 |
点评:本题考查的知识点是棱棱的体积,其中根据已知条件,计算出棱锥的底面面积,及结合正四棱锥中h=
(其中h为棱锥的高,H为棱锥的侧高,a为底面的棱长)求出棱锥的高,是解答本题的关键.
H2-(
|

练习册系列答案
相关题目
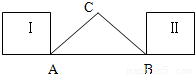
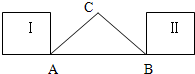 如图,在△ABC中,∠C=90°,
如图,在△ABC中,∠C=90°,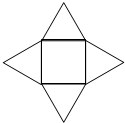 如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为________.
如图由一个边长为2的正方形及四个正三角形构成,将4个正三角形沿着其与正方形的公共边折起后形成的四棱锥的体积为________.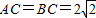 ,一个边长为2的正方形由位置Ⅰ沿AB平行移动到位置Ⅱ停止,若移动的距离为x,正方形和△ABC的公共部分的面积为f(x),试求出f(x)的解析式,并求出最大值.
,一个边长为2的正方形由位置Ⅰ沿AB平行移动到位置Ⅱ停止,若移动的距离为x,正方形和△ABC的公共部分的面积为f(x),试求出f(x)的解析式,并求出最大值.