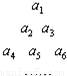题目内容
 已知集合A={3m+2n|m>n}且m,n∈N,若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )
已知集合A={3m+2n|m>n}且m,n∈N,若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )| A、247 | B、735 | C、733 | D、731 |
分析:根据题意可知,每一行所排的数成等差数列,只要求出前5行已经排了多少个数,就可以求出第六行第三个数是数列中的第几项,即可求得结果.
解答:解:该三角形数阵中,每一行所排的数成等差数列,首项为1,公差为1,
因此前5行已经排了
×5=15个数,
∴第六行第三个数是数列中的第18项,
∵a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…
∴a18=36+2×2=733,
故选C.
因此前5行已经排了
| 1+5 |
| 2 |
∴第六行第三个数是数列中的第18项,
∵a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…
∴a18=36+2×2=733,
故选C.
点评:考查根据已知条件分析数据、归纳能力,其中求出第六行第三个数是数列中的第18项,是解题的关键,属中档题.

练习册系列答案
相关题目
 已知集合A={3m+2n|m>n}且m,n∈N,若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为
已知集合A={3m+2n|m>n}且m,n∈N,若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33=27,…依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为