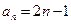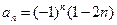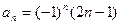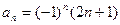题目内容
(本小题满分12分)
设数列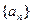 的前
的前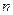 项和为
项和为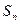 ,已知
,已知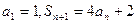
(1)设 ,证明数列
,证明数列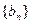 是等比数列;
是等比数列;
(2)求数列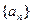 的通项公式.
的通项公式.
设数列
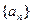 的前
的前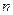 项和为
项和为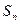 ,已知
,已知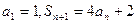
(1)设
 ,证明数列
,证明数列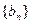 是等比数列;
是等比数列;(2)求数列
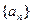 的通项公式.
的通项公式.(1)略
(2)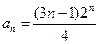
(2)
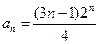
因为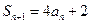 ,
,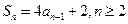
所以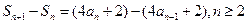
即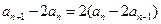 ,即
,即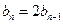 ,
,
又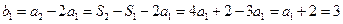
数列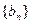 是等比数列
是等比数列
(2)因为数列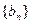 是首项为3,公比为2等比数列
是首项为3,公比为2等比数列
所以,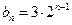 即有
即有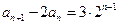 ,
,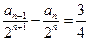
又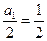 ,所以
,所以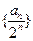 是首项为
是首项为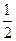 ,公差为
,公差为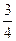 的等差数列
的等差数列
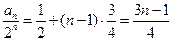
故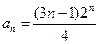
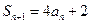 ,
,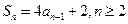
所以
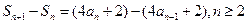
即
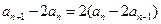 ,即
,即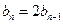 ,
,又
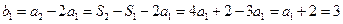
数列
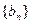 是等比数列
是等比数列(2)因为数列
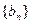 是首项为3,公比为2等比数列
是首项为3,公比为2等比数列所以,
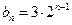 即有
即有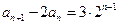 ,
,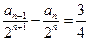
又
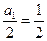 ,所以
,所以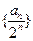 是首项为
是首项为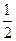 ,公差为
,公差为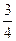 的等差数列
的等差数列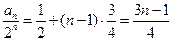
故
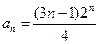

练习册系列答案
相关题目
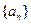 的前
的前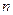 项和为
项和为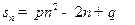 (
(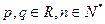 )
)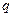 的值;
的值;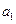 与
与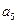 的等差中项为18,
的等差中项为18,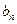 满足
满足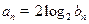 ,求数列
,求数列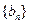 的前
的前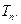
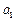 ,
,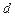 为实数,首项为
为实数,首项为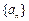 的前n项和为
的前n项和为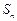 ,满
,满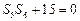 .(1)若
.(1)若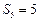 ,求
,求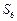 及
及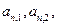 ……
……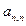 (n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则
(n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则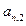 (n
(n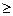 2且n
2且n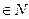 )的表达式
)的表达式
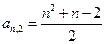
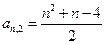
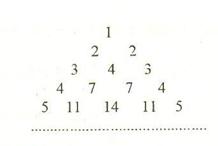
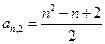
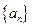 中,
中,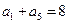 ,
,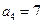 ,则
,则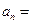 。
。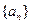 中,
中,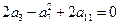 ,数列
,数列 是等比数列,且
是等比数列,且
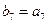 ,则
,则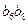 =" " ( ※ )
=" " ( ※ )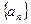 中,
中,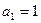 ,
,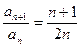 ,则其通项公式
,则其通项公式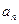 =
=