题目内容
(本小题满分15分)
设函数 与
与 的图像分别交直线
的图像分别交直线 于点
于点 ,且曲线
,且曲线 在点
在点 处的切线与曲线
处的切线与曲线 在点
在点 处的切线平行.
处的切线平行.
(1)求函数 ,
, 的表达式;
的表达式;
(2)设函数 ,求函数
,求函数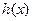 的最小值;
的最小值;
(3)若不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
设函数
 与
与 的图像分别交直线
的图像分别交直线 于点
于点 ,且曲线
,且曲线 在点
在点 处的切线与曲线
处的切线与曲线 在点
在点 处的切线平行.
处的切线平行.(1)求函数
 ,
, 的表达式;
的表达式;(2)设函数
 ,求函数
,求函数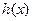 的最小值;
的最小值;(3)若不等式
 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.(1)由 得
得 ,由
,由 得
得 .又由题意可得
.又由题意可得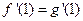 ,
,
即 ,故
,故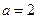 ,所以
,所以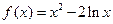 ,
, .
.
(2) 得
得
 .
.
由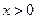 可知
可知 .故当
.故当 时
时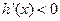 ,
,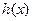 递减,当
递减,当
 时
时 ,
,
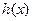 递增,所以函数
递增,所以函数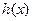 的最小值为
的最小值为 .
.
(3)当 时,
时, ,而
,而 ,故:
,故:
当 时,不等式
时,不等式 在
在 均成立.
均成立.
当 时,
时, 的最大值为
的最大值为 ,故要使
,故要使 恒成立,则必需
恒成立,则必需 ,即
,即 .事实上,当
.事实上,当 时,
时, .故可知此时
.故可知此时 .
.
综上可知当 时,不等式
时,不等式 在
在 均成立.
均成立.
 得
得 ,由
,由 得
得 .又由题意可得
.又由题意可得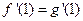 ,
,即
 ,故
,故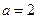 ,所以
,所以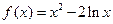 ,
, .
.(2)
 得
得 .
.由
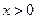 可知
可知 .故当
.故当 时
时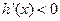 ,
,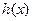 递减,当
递减,当 时
时 ,
,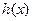 递增,所以函数
递增,所以函数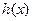 的最小值为
的最小值为 .
.(3)当
 时,
时, ,而
,而 ,故:
,故:当
 时,不等式
时,不等式 在
在 均成立.
均成立.当
 时,
时, 的最大值为
的最大值为 ,故要使
,故要使 恒成立,则必需
恒成立,则必需 ,即
,即 .事实上,当
.事实上,当 时,
时, .故可知此时
.故可知此时 .
.综上可知当
 时,不等式
时,不等式 在
在 均成立.
均成立.略

练习册系列答案
相关题目
 且
且 ,则
,则 ,得
,得 的一个周期为2,类比上述结论,请写出下列两个函数的一个周期.
的一个周期为2,类比上述结论,请写出下列两个函数的一个周期. 为正的常数,
为正的常数, ,求
,求 ,求
,求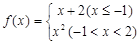 ,若
,若 f(a) =3 ,则a的取值为 ( )
f(a) =3 ,则a的取值为 ( )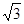
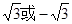
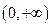 内是增函数,又
内是增函数,又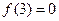 ,则
,则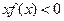 的解集是( )
的解集是( ) ;
;
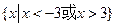 ;
; 
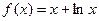 的零点所在的区间为 ( )w.
的零点所在的区间为 ( )w. ,1)
,1) )
) C上的函数满足
C上的函数满足 ,则
,则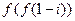 =
=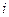
 (a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___
(a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是___ 对任意自然数x,y均满足:
对任意自然数x,y均满足: ,且
,且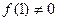 ,则
,则 等于( )
等于( )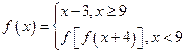 ,则
,则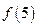 的值为
的值为