题目内容
从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:从9个数中随机抽取3个不同的数,共有C93种取法,3个数的和为偶数包括抽取3个数全为偶数,或抽取3数中2个奇数1个偶数,,用组合数表示出算式,根据古典概型公式得到结果.
解答:解:基本事件总数为C93,设抽取3个数,和为偶数为事件A,
则A事件数包括两类:抽取3个数全为偶数,
或抽取3数中2个奇数1个偶数,前者C43,后者C41C52.
∴A中基本事件数为C43+C41C52.
∴符合要求的概率为
=
.
则A事件数包括两类:抽取3个数全为偶数,
或抽取3数中2个奇数1个偶数,前者C43,后者C41C52.
∴A中基本事件数为C43+C41C52.
∴符合要求的概率为
| ||||||
|
| 11 |
| 21 |
点评:本题不能列举出基本事件,可以用组合数表示,如何判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数是解题的关键.

练习册系列答案
相关题目
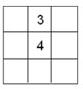 15、将1、2、3、…、9这九个数字填在如图所示的9个空格中,要求每一行
15、将1、2、3、…、9这九个数字填在如图所示的9个空格中,要求每一行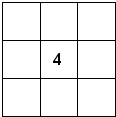 数字1,2,3,…,9这九条数字填写在如图所示的9个空格中,要求每一行从左到右依次增大,每一列从上到下也依次增大,当中心位置填上4后,所有填写空格的方法共有( )
数字1,2,3,…,9这九条数字填写在如图所示的9个空格中,要求每一行从左到右依次增大,每一列从上到下也依次增大,当中心位置填上4后,所有填写空格的方法共有( )