题目内容
 如图,是我国古代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,tan
如图,是我国古代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,tan| α |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
分析:由题意知小正方形的边长为2,大正方形的边长为10.设直角三角形中较小边长为x,根据图形可得较长边长为x+2,利用勾股定理列出关于x的方程,求出方程的解可得x的值,从而求出较长边及较小边的长度.运用正切函数定义得出tanα的值,然后利用二倍角的正切函数公式得出关于tan
的方程,求出方程的解即可求出tan
的值.
| α |
| 2 |
| α |
| 2 |
解答:解:由题意知,小正方形的边长为2,大正方形的边长为10.
设直角三角形中较小边长为x,
则有(x+2)2+x2=102,
解得,x=6.
∴较长边的边长为x+2=8.
∴tanα=
=
,又tanα=
,
可得:
=
,即(3tan
-1)(tan
+3)=0,
解得:tan
=
,tan
=-3(舍去),
则tan
=
.
故答案为:
设直角三角形中较小边长为x,
则有(x+2)2+x2=102,
解得,x=6.
∴较长边的边长为x+2=8.
∴tanα=
| 6 |
| 8 |
| 3 |
| 4 |
2tan
| ||
1-tan2
|
可得:
2tan
| ||
1-tan2
|
| 3 |
| 4 |
| α |
| 2 |
| α |
| 2 |
解得:tan
| α |
| 2 |
| 1 |
| 3 |
| α |
| 2 |
则tan
| α |
| 2 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题属于解三角形的题型,涉及的知识有:勾股定理,正方形的性质,锐角三角函数定义以及二倍角的正切函数公式,在求出tan
的值后,应根据
为锐角,对其值作出合理的取舍.
| α |
| 2 |
| α |
| 2 |

练习册系列答案
相关题目
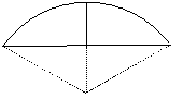 《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=
 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.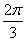 ,弦长等于9米的弧田.
,弦长等于9米的弧田.
 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差. ,弦长等于9米的弧田.
,弦长等于9米的弧田.
 ,那么
,那么 的值为
;
的值为
;