题目内容
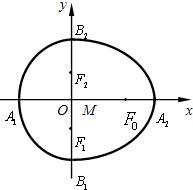
 如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(b>r>0).
如图,椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心为M(0,r)(b>r>0).
(1)写出椭圆的方程,求椭圆的焦点坐标及离心率.
(2)直线y=k1x交椭圆于两点C(x1,y1),D(x2,y2)(y2>0);直线y=k2x交椭圆于两点G(x3,y3),H(x4,y4)(y4>0).
求证: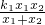 =
=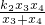 .
.
(3)对于(2)中的C、D、G、H,设CH交x轴于点P,GD交x轴于点Q.
求证:|OP|=|OQ|.
(证明过程不考虑CH或GD垂直于x轴的情形)
解:(1)如图可知椭圆的方程为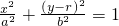
焦点坐标为F1(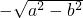 ,r),F2(
,r),F2( ,r)
,r)
离心率e=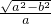
(2)将直线CD的方程y=k1x代入椭圆方程,
得b2x2+a2(k1x-r)2=a2b2,
整理得(b2+a2k12)x2-2k1a2rx+(a2r2-a2b2)=0.
根据韦达定理,得 x1+x2=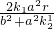
x1x2=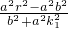
所以 =
=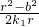 ①
①
将直线GH的方程y=k2x代入椭圆方程,同理可得
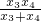 =
=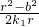 ②
②
由①,②得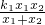 =
=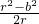 =
=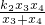 所以结论成立.
所以结论成立.
(3)设点P(p,0),点Q(q,0).
由C,P,H共线,得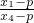 =
=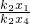
解得p=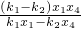
由D,Q,G共线,同理可得q=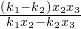
由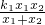 =
=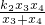 变形得
变形得
-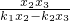 =
=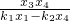
即-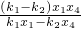 =
=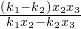
所以|p|=|q|,
即|OP|=|OQ|.
分析:(1)如图可知椭圆的顶点坐标,根据椭圆的性质可分别得出椭圆的长半轴和短半轴,进而得到椭圆的方程.再根据椭圆中a,b,c的关系求得c,进而可得椭圆的焦点和离心率.
(2)将直线CD的方程y=k1x代入椭圆方程,整理后根据韦达定理求得x1+x2和x1x2的值,两式相除可得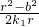 =
= ,同理可得
,同理可得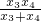 =
=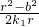 ,整理后进而可得
,整理后进而可得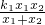 =
=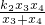 .
.
(3)设点P(p,0),点Q(q,0),根据C,P,H共线,得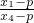 =
=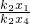 ,求得p;同样的方法求得q,由
,求得p;同样的方法求得q,由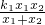 =
=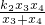 变形后即可证明所以|p|=|q|,原式得证.
变形后即可证明所以|p|=|q|,原式得证.
点评:本题主要考查了椭圆的方程和直线与椭圆的关系.考查了学生分析问题和综合运用知识的能力.是高考题出题的常用模式.
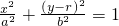
焦点坐标为F1(
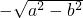 ,r),F2(
,r),F2( ,r)
,r)离心率e=
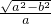
(2)将直线CD的方程y=k1x代入椭圆方程,
得b2x2+a2(k1x-r)2=a2b2,
整理得(b2+a2k12)x2-2k1a2rx+(a2r2-a2b2)=0.
根据韦达定理,得 x1+x2=
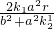
x1x2=
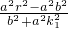
所以
 =
=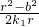 ①
①将直线GH的方程y=k2x代入椭圆方程,同理可得
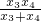 =
=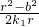 ②
②由①,②得
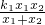 =
=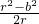 =
=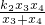 所以结论成立.
所以结论成立.(3)设点P(p,0),点Q(q,0).
由C,P,H共线,得
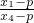 =
=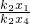
解得p=
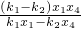
由D,Q,G共线,同理可得q=
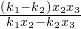
由
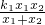 =
=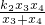 变形得
变形得-
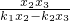 =
=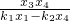
即-
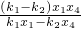 =
=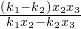
所以|p|=|q|,
即|OP|=|OQ|.
分析:(1)如图可知椭圆的顶点坐标,根据椭圆的性质可分别得出椭圆的长半轴和短半轴,进而得到椭圆的方程.再根据椭圆中a,b,c的关系求得c,进而可得椭圆的焦点和离心率.
(2)将直线CD的方程y=k1x代入椭圆方程,整理后根据韦达定理求得x1+x2和x1x2的值,两式相除可得
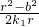 =
= ,同理可得
,同理可得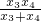 =
=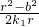 ,整理后进而可得
,整理后进而可得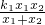 =
=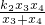 .
.(3)设点P(p,0),点Q(q,0),根据C,P,H共线,得
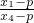 =
=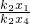 ,求得p;同样的方法求得q,由
,求得p;同样的方法求得q,由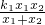 =
=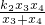 变形后即可证明所以|p|=|q|,原式得证.
变形后即可证明所以|p|=|q|,原式得证.点评:本题主要考查了椭圆的方程和直线与椭圆的关系.考查了学生分析问题和综合运用知识的能力.是高考题出题的常用模式.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 已知半椭圆
已知半椭圆 如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子: (2006•海淀区一模)如图,椭圆
(2006•海淀区一模)如图,椭圆
