题目内容
(满分16分)
记函数f(x)的定义域为D,若存在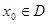 ,使
,使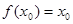 成立,则称以
成立,则称以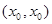 为坐标的点为函数
为坐标的点为函数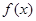 图象上的不动点。
图象上的不动点。
(1)若函数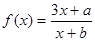 的图象上有两个关于原点对称的不动点,求
的图象上有两个关于原点对称的不动点,求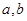 应满足的条件;
应满足的条件;
(2)下述结论“若定义在R上的奇函数f(x)的图象上存在有限个不动点,则不动点有奇数个”是否正确?若正确,请给予证明,并举出一例;若不正确,请举出一反例说明
【答案】
(1)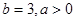
(2)证明略
【解析】
解:(1)由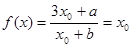 , …………………………………………2分
, …………………………………………2分
整理得  ……………………………………4分
……………………………………4分
由题意知方程(*)有两个互为相反数的根,所以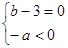 即
即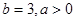 ………6分
………6分
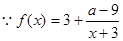 ,
,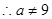 ,……………………………………………………8分
,……………………………………………………8分
故 应满足
应满足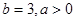 且
且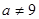 ……………………………………………………10分
……………………………………………………10分
(2)结论正确。……………………………………………………12分
证明: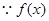 为奇函数,
为奇函数,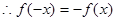 ,取
,取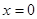 ,得
,得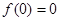 ,
,
即(0,0)为函数的一个不动点,设函数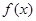 除0以外还有不动点
除0以外还有不动点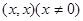 ,
,
则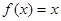
又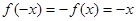 ,故
,故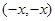 也为函数的不动点。…………………14分
也为函数的不动点。…………………14分
综上,若定义在R上的奇函数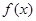 图象上存在有限个不动点,则不动点有奇数个。
图象上存在有限个不动点,则不动点有奇数个。
例如: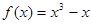 。…………………………………………………16分
。…………………………………………………16分

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目