题目内容
(08年永定一中二模文)(12分)
已知方向向量![]() 的直线
的直线![]() 过点
过点![]() 和椭圆
和椭圆![]() 的焦点,且椭圆C的中心O和椭圆的右准线上的点B满足:
的焦点,且椭圆C的中心O和椭圆的右准线上的点B满足:![]() .
.
(1)求椭圆C的方程;
(2)设![]() 、
、![]() 是椭圆C上两个不同点,且
是椭圆C上两个不同点,且![]() 、
、![]() 的纵坐标之和为1,记
的纵坐标之和为1,记![]() 为
为![]() 、
、![]() 横坐标之积,问是否存在最小的常数
横坐标之积,问是否存在最小的常数![]() ,使
,使![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解析:(1)![]()
![]() 与B点关于直线
与B点关于直线![]() 对称.
对称.
又![]() ……………………①
……………………①
![]() 过原点垂直于
过原点垂直于![]() 的直线为
的直线为![]() ………………②
………………②
由①②得![]() .
.
![]() 椭圆中心
椭圆中心![]() 的对称点在椭圆的右准线上.
的对称点在椭圆的右准线上.
![]() 又
又![]() 过焦点
过焦点 ![]()
![]()
故椭圆c的方程为![]() . …………………………………………………………6分
. …………………………………………………………6分
(2)若直线![]() 不含题意,若直线MN不平行于y轴,则设直线MN的方程为
不含题意,若直线MN不平行于y轴,则设直线MN的方程为![]() ,设
,设![]() .
.
由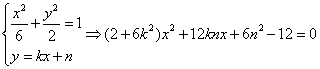 ……………………………………8分
……………………………………8分
![]()
即![]() ……………………①
……………………①
则![]()
由已知![]() ①得
①得
![]() ……………………………………………………………………10分
……………………………………………………………………10分
![]()
![]() 上增函数.
上增函数.
故![]() 故存在最小常数
故存在最小常数![]() …………………………12分
…………………………12分

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
