题目内容
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在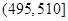 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.

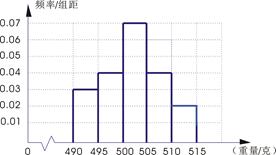
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
附:下面的临界值表供参考:
(参考公式: ,其中
,其中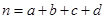 )
)
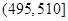 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.

表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面
 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 |  | 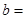 | |
| 不合格品 |  |  | |
| 合 计 | | | 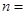 |
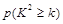 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中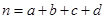 )
)
(1)
(2)甲样本合格品的频率为
乙样本合格品的频率为 ,
,
(3)90%的把握认为产品的包装质量与两条自动包装流水线的选择有关

(2)甲样本合格品的频率为

乙样本合格品的频率为
 ,
,(3)90%的把握认为产品的包装质量与两条自动包装流水线的选择有关
试题分析:(1)甲流水线样本的频率分布直方图如下:

6分
(2)由表1知甲样本中合格品数为
 ,由图1知乙样本中合格品数为
,由图1知乙样本中合格品数为 ,故甲样本合格品的频率为
,故甲样本合格品的频率为
乙样本合格品的频率为
 ,
,据此可估计从甲流水线任取1件产品,该产品恰好是合格品的概率为
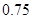
从乙流水线任取1件产品,该产品恰好是合格品的概率为
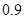 . 8分
. 8分(3)
 列联表如下:
列联表如下:| | 甲流水线 | 乙流水线 | 合计 |
| 合格品 |  30 30 |  36 36 | 66 |
| 不合格品 |  10 10 |  4 4 | 14 |
| 合 计 | 40 | 40 |  80 80 |
∵
 =
=
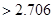
∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关. 14分
点评:解决的关键是根据直方图的概念和独立性检验的公式来得到,属于基础题。

练习册系列答案
相关题目
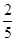 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是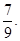
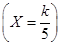 =
=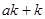 (
(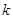 =1,2,3,4,5).
=1,2,3,4,5).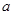 的值;
的值;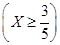 ;
;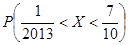
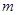 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为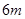 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是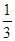 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?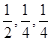 ,现有3名学生从中任选一个科目参加学习(互不影响),记
,现有3名学生从中任选一个科目参加学习(互不影响),记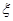 为3人中选择的科目属于“文学”或“竞赛”的人数,求
为3人中选择的科目属于“文学”或“竞赛”的人数,求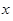 的分布列及期望。
的分布列及期望。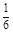 .甲、乙、丙三位同学每人购买了一瓶该饮料.
.甲、乙、丙三位同学每人购买了一瓶该饮料. ,求随机变量
,求随机变量