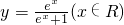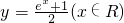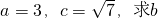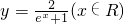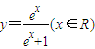题目内容
函数y=lnx-ln(1-x)(0<x<1)的反函数是( )
A、y=
| ||
B、y=
| ||
C、a=3,c=
| ||
D、y=
|
分析:根据求反函数的方法先把x用y表示出来,再交换x,y的位置既得所求的反函数.
解答:解:由题意y=ln
,得
=ey,
即得
=-1+
=ey,
∴1-x=
,
∴x=1-
=
,
∴函数y=lnx-ln(1-x)(0<x<1)的反函数是y=
(x∈R)
故选A
| x |
| 1-x |
| x |
| 1-x |
即得
| 1-(1-x) |
| 1-x |
| 1 |
| 1-x |
∴1-x=
| 1 |
| 1+ey |
∴x=1-
| 1 |
| 1+ey |
| ey |
| 1+ey |
∴函数y=lnx-ln(1-x)(0<x<1)的反函数是y=
| ex |
| ex+1 |
故选A
点评:本题考查反函数的求法,掌握好反函数的定义即可解好此类题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把函数y=lnx的图象按向量
=(-2,3)平移后得到y=f(x)的图象,则y=f(x)为( )
| a |
| A、ln(x+2)+3 |
| B、ln(x+2)-3 |
| C、ln(x-2)+3 |
| D、ln(x-2)-3 |
 已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如图所示,f(x)=lnx-h(x).
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如图所示,f(x)=lnx-h(x).